정보이론 Information Theory

머신러닝의 이론적 토대를 이룬다.

목차

  1. 정보이론의 이해

  2. Entorpy

  3. KL divergence

0. 정보이론의 이해

정보이론이란

추상적인 ‘정보’ 라는 개념을 정량화, 구체화 하는 분야이다.

image1

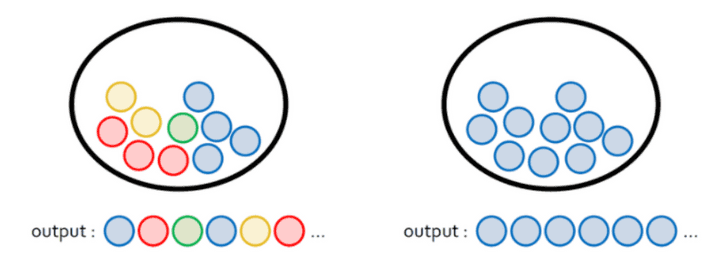
자 이런 두 개의 바구니에서

정보의 양이 더 많은 쪽은 어디일까?

왼쪽이다. 나올 수 있는 경우의 수가 더 많기 때문이다.

이건 다시말해서, 나올 수 있는 확률이 더 많다는 뜻이다.

그렇다면

왼쪽은 그대로 두고, 오른쪽 바구니에 빨간색 공 하나를 추가한다면?

그럼 파란색 공이 뽑힐 확률은 줄어들고 빨간색 공이 뽑힐 확률이 새로 생길 것이다.

이 두가지 중에서는 빨간색 공이 뽑힐 확률이 더 적다. 정보량은 확률을 가진 것 중에서도 적은 확률일 수록 높다.

Goodfellow, Bengio, Courville의 책 Deep Learning에는 정보를
정량적으로 표현하기 위해 필요한 세 가지 조건이 설명되어 있다.

  1. 일어날 가능성이 높으면 정보량이 적다,
  2. 일어날 가능서이 낮으면 정보량이 높다.
  3. 두 개의 독립적인 사건의 전체 정보량은 두 정보량의 합이다.

일반적으로 사건 x 가 일어날 확률을 p ( X = x) 라고 한다.

이때 사건의 정보량 I(x) 는

I(x) = -log P(x)

이때 log 의 ‘밑’은 2,e, 10 중 하나를 써도 무방하다

image2

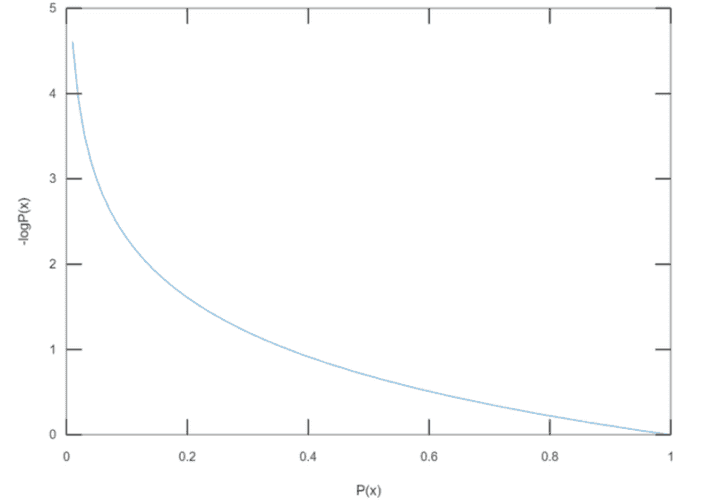
x가 일어날 확률이 1에 가까울수록 정보량은 줄어들고 있다.

import numpy as np
import math
import random

# 주머니 속에 들어있는 공의 개수입
total = 1000

#---------------#

count = 1   # 실험이 끝날 때까지 꺼낸 공의 개수

# 1부터 total까지의 정수 중에서 하나를 뽑고 total과 같으면 실험 종료
# total=1000인 경우 1~999: blue / 1000: red
while True:
    sample = random.randrange(1,total+1)
    if sample == total:
        break
    count += 1

print('number of blue samples: '+str(count-1))
print('information content: '+str(-math.log(1/count)))
number of blue samples: 1080
information content: 6.985641817639208

다음의 코드는 total 개의 수 중 total 번째의 수가 나오는 확률의 정보량이다.

사후확률의 정보량은 계속 변화하는 것을 알 수 있다.
허나 정보량은 사전확률을 기반으로 계산하기 때문에 변하지 않는 하나의 값이다.

이렇게 하나의 사건만 다루는 것도 있지만, 사실 세상은 그리 단순하지 않다

여러가지 변수가 있는 실험의 정보량은 어떻게 구할까?
이를 위해 엔트로피라는 개념이 필요하다

2. 엔트로피

확률변수가 가지는 모든 경우의 수
에 대해서
정보량을 각각 구한 다음 평균을 내면

평균적인 정보량을 알 수가 있는데, 이를 엔트로피 라고 한다.

Entrophy

이산 확률 변수 X 가 x1, x2,… xn 의 값을 가지는 경우에

엔트로피는 각각의 경우의 수가 가지는 정보량에 확률을 곱한 후,
그 값을 모두 더한 값이다.

image3

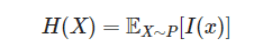
X들의 모든 정보량을 더해서 평균낸 값 = H(x)

image4

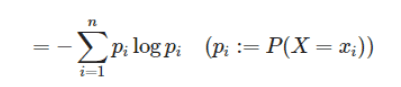
는 줄여서 이렇게 말할 수 잇다.

image5

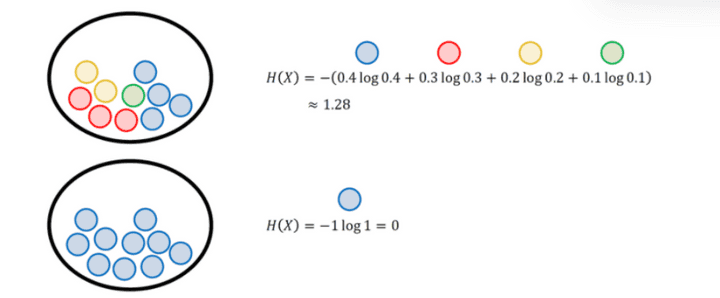
이렇게 하면 모든 정보량을 합친 엔트로피를 구할 수가 있는 것이다~

자 그럼 빨간공 한 개 있는건 어떻게 될까

image6

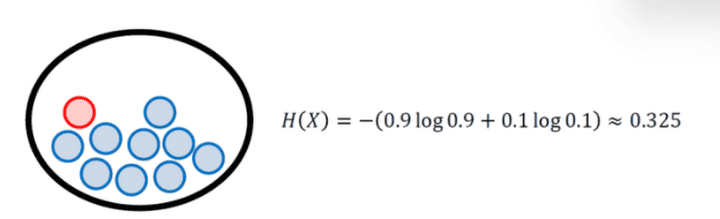
이렇게 엔트로피가 오른다!

나올수 있는 확률들의 값이 동등할수록 엔트로피의 값은 오른다.

어찌보면 당연하다

맨날 앞면만 나오는 동전보다
앞뒤가 동등하게 나오는 동전이
더 불확실하기 때문이다.

근데 이건 이산확률 변수일때만 가능 (끊어진 값 변수) 하다.

연속 확률 변수 일 때면?

합을 구하는 게 아니라 적분을 구한다.
개념적으로 생각해보면 당연하다. 그 사이의 모든 구역의 넓이를 구하는 것이기 때문이다.

image7

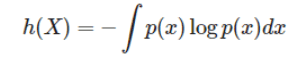
그냥 딱 더하는 걸 적분으로 바꿔주기만 하면 된다.

연속확률변수의 엔트로피는 이산확률분포의 엔트로피와 구분하기 위해

미분 엔트로피 라고 부른다.

머신러닝의 목표는 새로운 입력 데이터가 들어와도 예측이 잘 되도록, 모델의 확률 분포를 데이터의 실제 확률 분포에 가깝게 만드는 것

머신러닝 모델은 목적에 따라 크게 두가지로 나눌 수 있다.

  1. 생성모델

: 데이터와 모델로 도출할 수 있는 분포를 이용해 데이터의 실제 분포를 모델링

  1. 판별모델

: 데이터가 나뉘는 결정경계 (Decision Boundary) 를 학습.

특히 생성모델은 나올 수있는 모든 확률분포를 이용하는데, 이 때 확률 분포 간 차이를
평가하기 위해 쿨백-라이블러 발산 지표를 이용한다.

3. KL divergence (쿨백라이블러 발산)

Kullback-Leibler divergence. ; KL divergence

데이터의 실제 확률분포를 P(x)
모델이 나타낸 확률분포를 Q(x) 라 할 때,

KL divergence 는 다음과 같이 구한다.

P(x) 가 실제 확률분포라고 생각했을 때 Q(x) 의 엔트로피 에서 Q(x) 가 실제 확률분포라고 생각했을 때 P(x) 의 엔트로피 를 뺀다.

이것이 Q(x) 를 사용했을 때 발생하는 엔트로피의 변화량 KL-divergence 이다.

image8

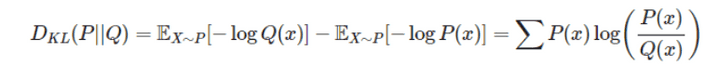
파란색 부분은 실제 분포이므로 우리가 바꿀 수 없다.

우리가 KL-D 값을 줄이기 위해서는 엔트로피의 변화량을 줄여야 하며, 결과적으로는 Q(x) 의 값을 P(x)의 값에 유사하게 만들어야 한다.

연속변수 에서는 식이 좀 다른데, 교차엔트로피를 구해야 한다.

image9

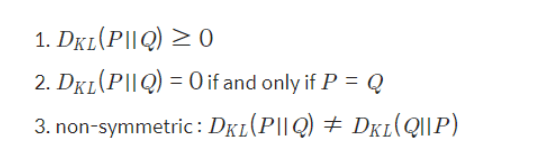
결과적으로 KL-D 로부터 엔트로피와 교차엔트로피를 다 구할 수 있다.

image10 image12

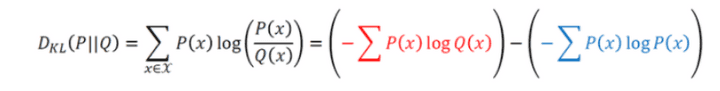
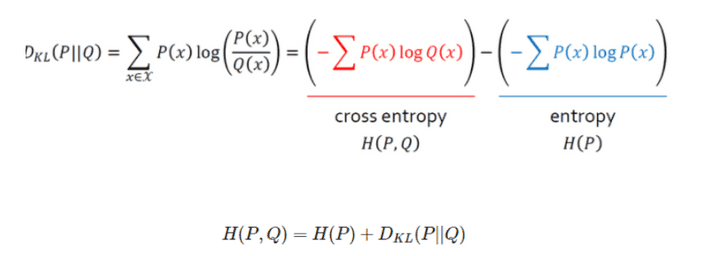
이렇게 해서 우리는
정답셋의 확률분포 P와
추론 결과의 확률분포 Q 의 차이

KL divergence를 최소화하는 것,

즉 우리 모델의 추론 결과가 정답셋과 최대한 유사하게 하는 것과
교차 엔트로피(Cross Entropy)를 최소화하는 것이 수학적으로 같다는 것을 확인했다.