정규화 정칙화 차이
정규화(라고 다같은 정규화가 아니다)
Regularization : 정칙화라고 불리며, 오버피팅을 해결하기 위한 방법 중의 하나
Regularization 기법들은 모델이 train set의 정답을 맞히지 못하도록 오버피팅을 방해(train loss가 증가) 하는 역할을 합니다. 그래서 train loss는 약간 증가하지만 결과적으로, validation loss나 최종적인 test loss를 감소시키려는 목적
(이건 오버피팅 방지)
Normalization : 정규화라고 불리며, 이는 데이터의 형태를 좀 더 의미 있게, 혹은 트레이닝에 적합하게 전처리하는 과정
(이건 전처리)
예를 들어
- 데이터를 z-socre 변환
- 0 과 1 사이 값으로 분포 조정
from sklearn.datasets import load_iris
import pandas as pd
import matplotlib.pyplot as plt
iris = load_iris()
iris_df = pd.DataFrame(data=iris.data, columns=iris.feature_names)
target_df = pd.DataFrame(data=iris.target, columns=['species'])
# 0, 1, 2로 되어있는 target 데이터를
# 알아보기 쉽게 'setosa', 'versicolor', 'virginica'로 바꿉니다
def converter(species):
if species == 0:
return 'setosa'
elif species == 1:
return 'versicolor'
else:
return 'virginica'
target_df['species'] = target_df['species'].apply(converter)
iris_df = pd.concat([iris_df, target_df], axis=1)
iris_df.head()| sepal length (cm) | sepal width (cm) | petal length (cm) | petal width (cm) | species | |
|---|---|---|---|---|---|
| 0 | 5.1 | 3.5 | 1.4 | 0.2 | setosa |
| 1 | 4.9 | 3.0 | 1.4 | 0.2 | setosa |
| 2 | 4.7 | 3.2 | 1.3 | 0.2 | setosa |
| 3 | 4.6 | 3.1 | 1.5 | 0.2 | setosa |
| 4 | 5.0 | 3.6 | 1.4 | 0.2 | setosa |
X = [iris_df['petal length (cm)'][a] for a in iris_df.index if iris_df['species'][a]=='virginica']
Y = [iris_df['sepal length (cm)'][a] for a in iris_df.index if iris_df['species'][a]=='virginica']
print(X)
print(Y)[6.0, 5.1, 5.9, 5.6, 5.8, 6.6, 4.5, 6.3, 5.8, 6.1, 5.1, 5.3, 5.5, 5.0, 5.1, 5.3, 5.5, 6.7, 6.9, 5.0, 5.7, 4.9, 6.7, 4.9, 5.7, 6.0, 4.8, 4.9, 5.6, 5.8, 6.1, 6.4, 5.6, 5.1, 5.6, 6.1, 5.6, 5.5, 4.8, 5.4, 5.6, 5.1, 5.1, 5.9, 5.7, 5.2, 5.0, 5.2, 5.4, 5.1]
[6.3, 5.8, 7.1, 6.3, 6.5, 7.6, 4.9, 7.3, 6.7, 7.2, 6.5, 6.4, 6.8, 5.7, 5.8, 6.4, 6.5, 7.7, 7.7, 6.0, 6.9, 5.6, 7.7, 6.3, 6.7, 7.2, 6.2, 6.1, 6.4, 7.2, 7.4, 7.9, 6.4, 6.3, 6.1, 7.7, 6.3, 6.4, 6.0, 6.9, 6.7, 6.9, 5.8, 6.8, 6.7, 6.7, 6.3, 6.5, 6.2, 5.9]plt.figure(figsize=(5,5))
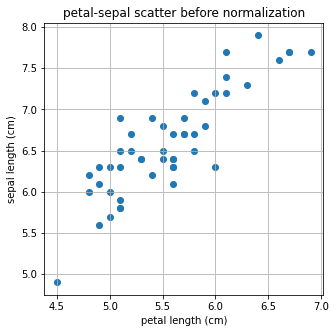
plt.scatter(X,Y)
plt.title('petal-sepal scatter before normalization')
plt.xlabel('petal length (cm)')
plt.ylabel('sepal length (cm)')
plt.grid()
plt.show()
from sklearn.preprocessing import minmax_scale
#sklearn 에서 지원하는 minmax_SCALE 로 0~ 1값으로 조정됨
X_scale = minmax_scale(X)
Y_scale = minmax_scale(Y)
plt.figure(figsize=(5,5))
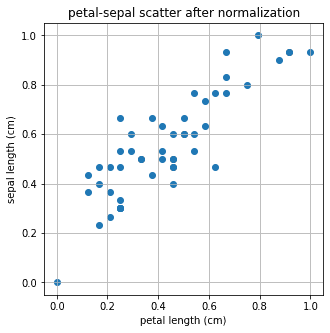
plt.scatter(X_scale,Y_scale)
plt.title('petal-sepal scatter after normalization')
plt.xlabel('petal length (cm)')
plt.ylabel('sepal length (cm)')
plt.grid()
plt.show()
from sklearn.linear_model import LinearRegression
import numpy as np
X = np.array(X)
Y = np.array(Y)
# Iris Dataset을 Linear Regression으로 학습합니다.
linear= LinearRegression()
linear.fit(X.reshape(-1,1), Y)
# Linear Regression의 기울기와 절편을 확인합니다.
a, b=linear.coef_, linear.intercept_
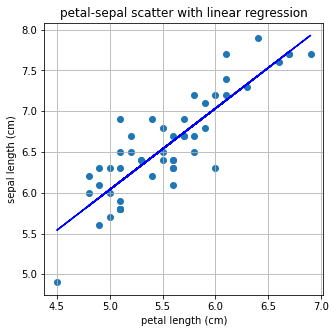
print("기울기 : %0.2f, 절편 : %0.2f" %(a,b))기울기 : 1.00, 절편 : 1.06plt.figure(figsize=(5,5))
plt.scatter(X,Y)
plt.plot(X,linear.predict(X.reshape(-1,1)),'-b')
plt.title('petal-sepal scatter with linear regression')
plt.xlabel('petal length (cm)')
plt.ylabel('sepal length (cm)')
plt.grid()
plt.show()
#L1 regularization은 Lasso로 import 합니다.
from sklearn.linear_model import Lasso
L1 = Lasso()
L1.fit(X.reshape(-1,1), Y)
a, b=L1.coef_, L1.intercept_
print("기울기 : %0.2f, 절편 : %0.2f" %(a,b))
plt.figure(figsize=(5,5))
plt.scatter(X,Y)
plt.plot(X,L1.predict(X.reshape(-1,1)),'-b')
plt.title('petal-sepal scatter with L1 regularization(Lasso)')
plt.xlabel('petal length (cm)')
plt.ylabel('sepal length (cm)')
plt.grid()
plt.show()기울기 : 0.00, 절편 : 6.59
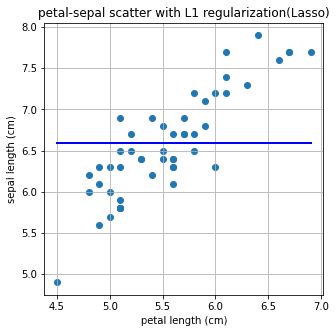
이게 Lasso 방식이고
#L2 regularization은 Ridge로 import 합니다.
from sklearn.linear_model import Ridge
L2 = Ridge()
L2.fit(X.reshape(-1,1), Y)
a, b = L2.coef_, L2.intercept_
print("기울기 : %0.2f, 절편 : %0.2f" %(a,b))
plt.figure(figsize=(5,5))
plt.scatter(X,Y)
plt.plot(X,L2.predict(X.reshape(-1,1)),'-b')
plt.title('petal-sepal scatter with L2 regularization(Ridge)')
plt.xlabel('petal length (cm)')
plt.ylabel('sepal length (cm)')
plt.grid()
plt.show()기울기 : 0.93, 절편 : 1.41
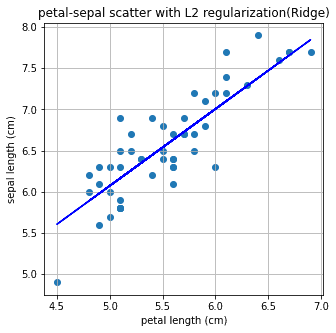
이게 Ridge 방법
기존 방법보다 축은 위로 쫌 이동했지만
기울기가 좀 줄었다
이 두 방식은 Regularization 다시말해 오버피팅을 방지한 것이다
, L1 Regularization을 사용할 때는 X가 2차원 이상인 여러 컬럼 값이 있는 데이터일 때 실제 효과를 볼 수 있습니다.
x가 1차원이었던 iris 꽃잎길이데이터같은 따분한거 쓰지말고
어른의 데이터인 wine dataset을 볼까?
from sklearn.datasets import load_wine
wine = load_wine()
wine_df = pd.DataFrame(data=wine.data, columns=wine.feature_names)
target_df = pd.DataFrame(data=wine.target, columns=['Y'])wine_df.head(5)| alcohol | malic_acid | ash | alcalinity_of_ash | magnesium | total_phenols | flavanoids | nonflavanoid_phenols | proanthocyanins | color_intensity | hue | od280/od315_of_diluted_wines | proline | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 14.23 | 1.71 | 2.43 | 15.6 | 127.0 | 2.80 | 3.06 | 0.28 | 2.29 | 5.64 | 1.04 | 3.92 | 1065.0 |
| 1 | 13.20 | 1.78 | 2.14 | 11.2 | 100.0 | 2.65 | 2.76 | 0.26 | 1.28 | 4.38 | 1.05 | 3.40 | 1050.0 |
| 2 | 13.16 | 2.36 | 2.67 | 18.6 | 101.0 | 2.80 | 3.24 | 0.30 | 2.81 | 5.68 | 1.03 | 3.17 | 1185.0 |
| 3 | 14.37 | 1.95 | 2.50 | 16.8 | 113.0 | 3.85 | 3.49 | 0.24 | 2.18 | 7.80 | 0.86 | 3.45 | 1480.0 |
| 4 | 13.24 | 2.59 | 2.87 | 21.0 | 118.0 | 2.80 | 2.69 | 0.39 | 1.82 | 4.32 | 1.04 | 2.93 | 735.0 |
target_df.head(5)| Y | |
|---|---|
| 0 | 0 |
| 1 | 0 |
| 2 | 0 |
| 3 | 0 |
| 4 | 0 |
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_absolute_error, mean_squared_error
# 데이터를 준비하고
X_train, X_test, y_train, y_test = train_test_split(wine_df, target_df, test_size=0.3, random_state=101)
# 모델을 훈련시킵니다.
model = LinearRegression()
model.fit(X_train, y_train)
# 테스트를 해볼까요?
model.predict(X_test)
pred = model.predict(X_test)
# 테스트 결과는 이렇습니다!
print("result of linear regression")
print('Mean Absolute Error:', mean_absolute_error(y_test, pred))
print('Mean Squared Error:', mean_squared_error(y_test, pred))
print('Mean Root Squared Error:', np.sqrt(mean_squared_error(y_test, pred)))
print("\n\n coefficient linear regression")
print(model.coef_)result of linear regression
Mean Absolute Error: 0.25128973939722626
Mean Squared Error: 0.1062458740952556
Mean Root Squared Error: 0.32595379134971814
coefficient linear regression
[[-8.09017190e-02 4.34817880e-02 -1.18857931e-01 3.65705449e-02
-4.68014203e-04 1.41423581e-01 -4.54107854e-01 -5.13172664e-01
9.69318443e-02 5.34311136e-02 -1.27626604e-01 -2.91381844e-01
-5.72238959e-04]]선형회귀로 문제를 풀고
계수(coefficient)
절대 오차 ( mean absolute error)
제곱 오차 ( mean squared error)
평균 제곱값 오차 (root mean squared error)
를 출력
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_absolute_error, mean_squared_error
# 데이터를 준비하고
X_train, X_test, y_train, y_test = train_test_split(wine_df, target_df, test_size=0.3, random_state=101)
# 모델을 훈련시킵니다.
model = LinearRegression()
model.fit(X_train, y_train)
# 테스트를 해볼까요?
model.predict(X_test)
pred = model.predict(X_test)
# 테스트 결과는 이렇습니다!
print("result of linear regression")
print('Mean Absolute Error:', mean_absolute_error(y_test, pred))
print('Mean Squared Error:', mean_squared_error(y_test, pred))
print('Mean Root Squared Error:', np.sqrt(mean_squared_error(y_test, pred)))
print("\n\n coefficient linear regression")
print(model.coef_)result of linear regression
Mean Absolute Error: 0.25128973939722626
Mean Squared Error: 0.1062458740952556
Mean Root Squared Error: 0.32595379134971814
coefficient linear regression
[[-8.09017190e-02 4.34817880e-02 -1.18857931e-01 3.65705449e-02
-4.68014203e-04 1.41423581e-01 -4.54107854e-01 -5.13172664e-01
9.69318443e-02 5.34311136e-02 -1.27626604e-01 -2.91381844e-01
-5.72238959e-04]]from sklearn.linear_model import Lasso
from sklearn.metrics import mean_absolute_error, mean_squared_error
# 모델을 준비하고 훈련시킵니다.
L1 = Lasso(alpha=0.05)
L1.fit(X_train, y_train)
# 테스트를 해봅시다.
pred = L1.predict(X_test)
# 모델 성능은 얼마나 좋을까요?
print("result of Lasso")
print('Mean Absolute Error:', mean_absolute_error(y_test, pred))
print('Mean Squared Error:', mean_squared_error(y_test, pred))
print('Mean Root Squared Error:', np.sqrt(mean_squared_error(y_test, pred)))
print("\n\n coefficient of Lasso")
print(L1.coef_)result of Lasso
Mean Absolute Error: 0.24233731936122138
Mean Squared Error: 0.0955956894578189
Mean Root Squared Error: 0.3091855259513597
coefficient of Lasso
[-0. 0.01373795 -0. 0.03065716 0.00154719 -0.
-0.34143614 -0. 0. 0.06755943 -0. -0.14558153
-0.00089635]coefficient 부분을 보시면 Linear Regression과 L1 Regularization의 차이가 좀 더 두드러짐
inear Regression에서는 모든 컬럼의 가중치를 탐색하여 구하는 반면, L1 Regularization에서는 총 13개 중 7개를 제외한 나머지의 값들이 모두 0임
L2 norm Ridge

보면 L1 은 걍 절댓값만 씌우고
L2 는 제곱을 해,,! 그 차이야,,!!

L2 는 제곱을 하기 때문에 저렇게 원의 형태가 나와
하지만 L1 은 사각형이지
제곱이라 수렴 속도도 빠름 더 가까운 길을 찾을 수 있잖아
정리하면, L1 Regularization은 가중치가 적은 벡터에 해당하는 계수를 0으로 보내면서 차원 축소와 비슷한 역할을 하는 것이 특징이며, L2 Regularization은 0이 아닌 0에 가깝게 보내지만 제곱 텀이 있기 때문에 L1 Regularization보다는 수렴 속도가 빠르다는 장점
예를 들어, A=[1,1,1,1,1]A=[1,1,1,1,1] , B=[5,0,0,0,0]B=[5,0,0,0,0] 의 경우
L1-norm은 같지만, L2-norm은 같지 않습니다.
즉, 제곱 텀에서 결과에 큰 영향을 미치는 값은 더 크게,
결과에 영향이 적은 값들은 더 작게 보내면서 수렴 속도가 빨라지는 것입니다.
그러므로, 데이터에 따라 적절한 Regularization 방법을 활용하는 것이 좋습니다.
근데 그래서 Norm 이란게 뭘까…?
- vector norm
- matrix norm
Norm이라는 개념은 벡터뿐만 아니라 함수, 행렬에 대해서 크기를 구하는 것으로, 딥러닝을 배우는 과정에서는 주로 벡터, 좀 더 어렵게는 행렬의 Norm 정도만 알면 됩니다.

- vector
x=np.array([1,10,1,1,1])
p=5
norm_x=np.linalg.norm(x, ord=p)
making_norm = (sum(x**p))**(1/p)
print("result of numpy package norm function : %0.5f "%norm_x)
print("result of making norm : %0.5f "%making_norm)result of numpy package norm function : 10.00008
result of making norm : 10.00008 - matrix
A=np.array([[1,2,3],[1,2,3],[4,6,8]])
inf_norm_A=np.linalg.norm(A, ord=np.inf)
print("result inf norm of A :", inf_norm_A)
one_norm_A=np.linalg.norm(A, ord=1)
print("result one norm of A :", one_norm_A)result inf norm of A : 18.0
result one norm of A : 14.0Dropout 은 뭔데?
Dropout 은 Regularization 으로 오버피팅을 막는 정칙화 이다.
fully connected layer에서 오버피팅이 생기는 경우에 주로 Dropout layer를 추가합니다.
import tensorflow as tf
from tensorflow import keras
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
fashion_mnist = keras.datasets.fashion_mnist
print('=3')=3(train_images, train_labels), (test_images, test_labels) = fashion_mnist.load_data()
class_names = ['T-shirt/top', 'Trouser', 'Pullover', 'Dress', 'Coat',
'Sandal', 'Shirt', 'Sneaker', 'Bag', 'Ankle boot']
train_images = train_images / 255.0
test_images = test_images / 255.0model = keras.Sequential([
keras.layers.Flatten(input_shape=(28, 28)),
keras.layers.Dense(128, activation='relu'),
# 여기에 dropout layer를 추가해보았습니다. 나머지 layer는 아래의 실습과 같습니다.
keras.layers.Dropout(0.9),
keras.layers.Dense(10, activation='softmax')
])
model.compile(optimizer='adam',loss='sparse_categorical_crossentropy',
metrics=['accuracy'])
history= model.fit(train_images, train_labels, epochs=5)Epoch 1/5
1875/1875 [==============================] - 5s 2ms/step - loss: 1.4060 - accuracy: 0.4571
Epoch 2/5
1875/1875 [==============================] - 4s 2ms/step - loss: 1.1796 - accuracy: 0.5296
Epoch 3/5
1875/1875 [==============================] - 4s 2ms/step - loss: 1.1358 - accuracy: 0.5459
Epoch 4/5
1875/1875 [==============================] - 4s 2ms/step - loss: 1.1104 - accuracy: 0.5530
Epoch 5/5
1875/1875 [==============================] - 4s 2ms/step - loss: 1.0902 - accuracy: 0.5628model = keras.Sequential([
keras.layers.Flatten(input_shape=(28, 28)),
# 이번에는 dropout layer가 없습니다.
keras.layers.Dense(128, activation='relu'),
keras.layers.Dense(10, activation='softmax')
])
model.compile(optimizer='adam',loss='sparse_categorical_crossentropy',
metrics=['accuracy'])
history = model.fit(train_images, train_labels, epochs=5)Epoch 1/5
1875/1875 [==============================] - 4s 2ms/step - loss: 0.5047 - accuracy: 0.8254
Epoch 2/5
1875/1875 [==============================] - 4s 2ms/step - loss: 0.3759 - accuracy: 0.8648
Epoch 3/5
1875/1875 [==============================] - 4s 2ms/step - loss: 0.3370 - accuracy: 0.8777
Epoch 4/5
1875/1875 [==============================] - 4s 2ms/step - loss: 0.3138 - accuracy: 0.8853
Epoch 5/5
1875/1875 [==============================] - 4s 2ms/step - loss: 0.2967 - accuracy: 0.8910보면 드랍아웃을 0.9로 주면 정확도가 56% 이다
아무것도 안한게 89% 인데 ㅋ 어이없어 저렇겐 쓰지마
근데 오버피팅 줄일때 써봐
overfitting 줄이는 법
X_train, X_valid, y_train, y_valid = train_test_split(train_images, train_labels, test_size=0.01, random_state=101)
X_train = X_train / 255.0
X_valid = X_valid / 255.0
#Dense layer만으로 만들어 낸 classification 모델입니다.
model = keras.Sequential([
keras.layers.Flatten(input_shape=(28, 28)),
keras.layers.Dense(256, activation='relu'),
keras.layers.Dense(10, activation='softmax')
])
model.compile(optimizer='adam',loss='sparse_categorical_crossentropy',
metrics=['accuracy'])
history= model.fit(X_train, y_train, epochs=200, batch_size=512, validation_data=(X_valid, y_valid))Epoch 1/200
117/117 [==============================] - 1s 5ms/step - loss: 2.0499 - accuracy: 0.5479 - val_loss: 1.6354 - val_accuracy: 0.5983
Epoch 2/200
117/117 [==============================] - 0s 4ms/step - loss: 1.3857 - accuracy: 0.6154 - val_loss: 1.1556 - val_accuracy: 0.6817
Epoch 3/200
117/117 [==============================] - 0s 4ms/step - loss: 1.0562 - accuracy: 0.6812 - val_loss: 0.9326 - val_accuracy: 0.7333
Epoch 4/200
117/117 [==============================] - 0s 4ms/step - loss: 0.8842 - accuracy: 0.7192 - val_loss: 0.8094 - val_accuracy: 0.7483
Epoch 5/200
117/117 [==============================] - 0s 4ms/step - loss: 0.7847 - accuracy: 0.7343 - val_loss: 0.7366 - val_accuracy: 0.7650
Epoch 6/200
117/117 [==============================] - 0s 4ms/step - loss: 0.7235 - accuracy: 0.7471 - val_loss: 0.6882 - val_accuracy: 0.7717
Epoch 7/200
117/117 [==============================] - 0s 4ms/step - loss: 0.6827 - accuracy: 0.7565 - val_loss: 0.6565 - val_accuracy: 0.7850
Epoch 8/200
117/117 [==============================] - 0s 3ms/step - loss: 0.6518 - accuracy: 0.7663 - val_loss: 0.6299 - val_accuracy: 0.7917
Epoch 9/200
117/117 [==============================] - 0s 4ms/step - loss: 0.6271 - accuracy: 0.7739 - val_loss: 0.6132 - val_accuracy: 0.7933
Epoch 10/200
117/117 [==============================] - 0s 3ms/step - loss: 0.6065 - accuracy: 0.7824 - val_loss: 0.5906 - val_accuracy: 0.7950
Epoch 11/200
117/117 [==============================] - 0s 3ms/step - loss: 0.5883 - accuracy: 0.7897 - val_loss: 0.5751 - val_accuracy: 0.7967
Epoch 12/200
117/117 [==============================] - 0s 4ms/step - loss: 0.5725 - accuracy: 0.7971 - val_loss: 0.5648 - val_accuracy: 0.8017
Epoch 13/200
117/117 [==============================] - 0s 4ms/step - loss: 0.5597 - accuracy: 0.8016 - val_loss: 0.5587 - val_accuracy: 0.8000
Epoch 14/200
117/117 [==============================] - 0s 4ms/step - loss: 0.5459 - accuracy: 0.8068 - val_loss: 0.5408 - val_accuracy: 0.8033
Epoch 15/200
117/117 [==============================] - 0s 3ms/step - loss: 0.5356 - accuracy: 0.8118 - val_loss: 0.5273 - val_accuracy: 0.8000
Epoch 16/200
117/117 [==============================] - 0s 4ms/step - loss: 0.5256 - accuracy: 0.8148 - val_loss: 0.5238 - val_accuracy: 0.8117
Epoch 17/200
117/117 [==============================] - 0s 4ms/step - loss: 0.5163 - accuracy: 0.8192 - val_loss: 0.5124 - val_accuracy: 0.8117
Epoch 18/200
117/117 [==============================] - 0s 3ms/step - loss: 0.5078 - accuracy: 0.8216 - val_loss: 0.5084 - val_accuracy: 0.8117
Epoch 19/200
117/117 [==============================] - 0s 3ms/step - loss: 0.5001 - accuracy: 0.8243 - val_loss: 0.5048 - val_accuracy: 0.8133
Epoch 20/200
117/117 [==============================] - 0s 4ms/step - loss: 0.4931 - accuracy: 0.8270 - val_loss: 0.4947 - val_accuracy: 0.8183
Epoch 21/200
117/117 [==============================] - 0s 4ms/step - loss: 0.4868 - accuracy: 0.8289 - val_loss: 0.4901 - val_accuracy: 0.8167
Epoch 22/200
117/117 [==============================] - 0s 4ms/step - loss: 0.4807 - accuracy: 0.8313 - val_loss: 0.4836 - val_accuracy: 0.8233
Epoch 23/200
117/117 [==============================] - 0s 4ms/step - loss: 0.4756 - accuracy: 0.8335 - val_loss: 0.4753 - val_accuracy: 0.8250
Epoch 24/200
117/117 [==============================] - 0s 3ms/step - loss: 0.4705 - accuracy: 0.8356 - val_loss: 0.4692 - val_accuracy: 0.8267
Epoch 25/200
117/117 [==============================] - 0s 4ms/step - loss: 0.4657 - accuracy: 0.8366 - val_loss: 0.4710 - val_accuracy: 0.8283
Epoch 26/200
117/117 [==============================] - 0s 3ms/step - loss: 0.4616 - accuracy: 0.8384 - val_loss: 0.4609 - val_accuracy: 0.8267
Epoch 27/200
117/117 [==============================] - 0s 3ms/step - loss: 0.4584 - accuracy: 0.8388 - val_loss: 0.4640 - val_accuracy: 0.8250
Epoch 28/200
117/117 [==============================] - 0s 4ms/step - loss: 0.4538 - accuracy: 0.8412 - val_loss: 0.4571 - val_accuracy: 0.8333
Epoch 29/200
117/117 [==============================] - 0s 4ms/step - loss: 0.4502 - accuracy: 0.8428 - val_loss: 0.4522 - val_accuracy: 0.8333
Epoch 30/200
117/117 [==============================] - 0s 4ms/step - loss: 0.4471 - accuracy: 0.8435 - val_loss: 0.4497 - val_accuracy: 0.8317
Epoch 31/200
117/117 [==============================] - 0s 4ms/step - loss: 0.4442 - accuracy: 0.8450 - val_loss: 0.4491 - val_accuracy: 0.8317
Epoch 32/200
117/117 [==============================] - 0s 4ms/step - loss: 0.4410 - accuracy: 0.8456 - val_loss: 0.4417 - val_accuracy: 0.8333
Epoch 33/200
117/117 [==============================] - 0s 4ms/step - loss: 0.4379 - accuracy: 0.8473 - val_loss: 0.4395 - val_accuracy: 0.8367
Epoch 34/200
117/117 [==============================] - 0s 3ms/step - loss: 0.4352 - accuracy: 0.8474 - val_loss: 0.4377 - val_accuracy: 0.8333
Epoch 35/200
117/117 [==============================] - 0s 3ms/step - loss: 0.4329 - accuracy: 0.8487 - val_loss: 0.4360 - val_accuracy: 0.8317
Epoch 36/200
117/117 [==============================] - 0s 3ms/step - loss: 0.4316 - accuracy: 0.8485 - val_loss: 0.4331 - val_accuracy: 0.8367
Epoch 37/200
117/117 [==============================] - 0s 4ms/step - loss: 0.4279 - accuracy: 0.8499 - val_loss: 0.4331 - val_accuracy: 0.8350
Epoch 38/200
117/117 [==============================] - 0s 4ms/step - loss: 0.4267 - accuracy: 0.8499 - val_loss: 0.4268 - val_accuracy: 0.8333
Epoch 39/200
117/117 [==============================] - 0s 4ms/step - loss: 0.4239 - accuracy: 0.8517 - val_loss: 0.4282 - val_accuracy: 0.8367
Epoch 40/200
117/117 [==============================] - 0s 3ms/step - loss: 0.4217 - accuracy: 0.8526 - val_loss: 0.4243 - val_accuracy: 0.8400
Epoch 41/200
117/117 [==============================] - 0s 4ms/step - loss: 0.4195 - accuracy: 0.8534 - val_loss: 0.4206 - val_accuracy: 0.8350
Epoch 42/200
117/117 [==============================] - 0s 3ms/step - loss: 0.4177 - accuracy: 0.8538 - val_loss: 0.4232 - val_accuracy: 0.8333
Epoch 43/200
117/117 [==============================] - 0s 3ms/step - loss: 0.4164 - accuracy: 0.8543 - val_loss: 0.4232 - val_accuracy: 0.8383
Epoch 44/200
117/117 [==============================] - 0s 4ms/step - loss: 0.4138 - accuracy: 0.8559 - val_loss: 0.4183 - val_accuracy: 0.8317
Epoch 45/200
117/117 [==============================] - 0s 4ms/step - loss: 0.4125 - accuracy: 0.8556 - val_loss: 0.4137 - val_accuracy: 0.8300
Epoch 46/200
117/117 [==============================] - 0s 4ms/step - loss: 0.4106 - accuracy: 0.8564 - val_loss: 0.4153 - val_accuracy: 0.8317
Epoch 47/200
117/117 [==============================] - 0s 3ms/step - loss: 0.4095 - accuracy: 0.8566 - val_loss: 0.4131 - val_accuracy: 0.8350
Epoch 48/200
117/117 [==============================] - 0s 3ms/step - loss: 0.4067 - accuracy: 0.8581 - val_loss: 0.4158 - val_accuracy: 0.8400
Epoch 49/200
117/117 [==============================] - 0s 3ms/step - loss: 0.4059 - accuracy: 0.8577 - val_loss: 0.4130 - val_accuracy: 0.8333
Epoch 50/200
117/117 [==============================] - 0s 3ms/step - loss: 0.4032 - accuracy: 0.8588 - val_loss: 0.4109 - val_accuracy: 0.8367
Epoch 51/200
117/117 [==============================] - 0s 3ms/step - loss: 0.4019 - accuracy: 0.8594 - val_loss: 0.4092 - val_accuracy: 0.8317
Epoch 52/200
117/117 [==============================] - 0s 3ms/step - loss: 0.4010 - accuracy: 0.8599 - val_loss: 0.4081 - val_accuracy: 0.8350
Epoch 53/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3985 - accuracy: 0.8603 - val_loss: 0.4027 - val_accuracy: 0.8333
Epoch 54/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3972 - accuracy: 0.8607 - val_loss: 0.4011 - val_accuracy: 0.8367
Epoch 55/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3959 - accuracy: 0.8609 - val_loss: 0.4045 - val_accuracy: 0.8367
Epoch 56/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3946 - accuracy: 0.8608 - val_loss: 0.3998 - val_accuracy: 0.8383
Epoch 57/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3925 - accuracy: 0.8622 - val_loss: 0.3959 - val_accuracy: 0.8367
Epoch 58/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3920 - accuracy: 0.8624 - val_loss: 0.3958 - val_accuracy: 0.8383
Epoch 59/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3905 - accuracy: 0.8628 - val_loss: 0.3966 - val_accuracy: 0.8350
Epoch 60/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3898 - accuracy: 0.8634 - val_loss: 0.3964 - val_accuracy: 0.8417
Epoch 61/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3877 - accuracy: 0.8642 - val_loss: 0.3943 - val_accuracy: 0.8333
Epoch 62/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3858 - accuracy: 0.8643 - val_loss: 0.3931 - val_accuracy: 0.8450
Epoch 63/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3848 - accuracy: 0.8643 - val_loss: 0.3928 - val_accuracy: 0.8433
Epoch 64/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3840 - accuracy: 0.8642 - val_loss: 0.3893 - val_accuracy: 0.8350
Epoch 65/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3822 - accuracy: 0.8652 - val_loss: 0.3940 - val_accuracy: 0.8367
Epoch 66/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3828 - accuracy: 0.8659 - val_loss: 0.3843 - val_accuracy: 0.8367
Epoch 67/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3800 - accuracy: 0.8664 - val_loss: 0.3837 - val_accuracy: 0.8383
Epoch 68/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3787 - accuracy: 0.8665 - val_loss: 0.3838 - val_accuracy: 0.8367
Epoch 69/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3773 - accuracy: 0.8672 - val_loss: 0.3854 - val_accuracy: 0.8367
Epoch 70/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3774 - accuracy: 0.8673 - val_loss: 0.3827 - val_accuracy: 0.8383
Epoch 71/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3752 - accuracy: 0.8684 - val_loss: 0.3791 - val_accuracy: 0.8367
Epoch 72/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3738 - accuracy: 0.8686 - val_loss: 0.3844 - val_accuracy: 0.8467
Epoch 73/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3740 - accuracy: 0.8677 - val_loss: 0.3817 - val_accuracy: 0.8467
Epoch 74/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3729 - accuracy: 0.8684 - val_loss: 0.3797 - val_accuracy: 0.8417
Epoch 75/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3706 - accuracy: 0.8687 - val_loss: 0.3812 - val_accuracy: 0.8467
Epoch 76/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3701 - accuracy: 0.8693 - val_loss: 0.3757 - val_accuracy: 0.8483
Epoch 77/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3689 - accuracy: 0.8693 - val_loss: 0.3788 - val_accuracy: 0.8450
Epoch 78/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3684 - accuracy: 0.8705 - val_loss: 0.3774 - val_accuracy: 0.8483
Epoch 79/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3680 - accuracy: 0.8703 - val_loss: 0.3738 - val_accuracy: 0.8433
Epoch 80/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3657 - accuracy: 0.8711 - val_loss: 0.3756 - val_accuracy: 0.8450
Epoch 81/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3648 - accuracy: 0.8716 - val_loss: 0.3760 - val_accuracy: 0.8450
Epoch 82/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3656 - accuracy: 0.8708 - val_loss: 0.3768 - val_accuracy: 0.8467
Epoch 83/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3628 - accuracy: 0.8719 - val_loss: 0.3718 - val_accuracy: 0.8467
Epoch 84/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3612 - accuracy: 0.8729 - val_loss: 0.3743 - val_accuracy: 0.8450
Epoch 85/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3608 - accuracy: 0.8727 - val_loss: 0.3700 - val_accuracy: 0.8417
Epoch 86/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3602 - accuracy: 0.8727 - val_loss: 0.3771 - val_accuracy: 0.8467
Epoch 87/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3612 - accuracy: 0.8727 - val_loss: 0.3671 - val_accuracy: 0.8450
Epoch 88/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3577 - accuracy: 0.8743 - val_loss: 0.3657 - val_accuracy: 0.8450
Epoch 89/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3569 - accuracy: 0.8745 - val_loss: 0.3677 - val_accuracy: 0.8500
Epoch 90/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3559 - accuracy: 0.8743 - val_loss: 0.3750 - val_accuracy: 0.8483
Epoch 91/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3563 - accuracy: 0.8748 - val_loss: 0.3626 - val_accuracy: 0.8400
Epoch 92/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3541 - accuracy: 0.8749 - val_loss: 0.3644 - val_accuracy: 0.8433
Epoch 93/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3536 - accuracy: 0.8752 - val_loss: 0.3652 - val_accuracy: 0.8467
Epoch 94/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3527 - accuracy: 0.8754 - val_loss: 0.3644 - val_accuracy: 0.8483
Epoch 95/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3514 - accuracy: 0.8757 - val_loss: 0.3615 - val_accuracy: 0.8500
Epoch 96/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3521 - accuracy: 0.8755 - val_loss: 0.3620 - val_accuracy: 0.8550
Epoch 97/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3505 - accuracy: 0.8756 - val_loss: 0.3613 - val_accuracy: 0.8467
Epoch 98/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3501 - accuracy: 0.8766 - val_loss: 0.3613 - val_accuracy: 0.8483
Epoch 99/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3491 - accuracy: 0.8769 - val_loss: 0.3630 - val_accuracy: 0.8533
Epoch 100/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3472 - accuracy: 0.8775 - val_loss: 0.3580 - val_accuracy: 0.8483
Epoch 101/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3466 - accuracy: 0.8775 - val_loss: 0.3561 - val_accuracy: 0.8433
Epoch 102/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3466 - accuracy: 0.8774 - val_loss: 0.3581 - val_accuracy: 0.8533
Epoch 103/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3458 - accuracy: 0.8783 - val_loss: 0.3562 - val_accuracy: 0.8467
Epoch 104/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3452 - accuracy: 0.8774 - val_loss: 0.3581 - val_accuracy: 0.8417
Epoch 105/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3444 - accuracy: 0.8783 - val_loss: 0.3597 - val_accuracy: 0.8517
Epoch 106/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3435 - accuracy: 0.8784 - val_loss: 0.3579 - val_accuracy: 0.8567
Epoch 107/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3440 - accuracy: 0.8782 - val_loss: 0.3545 - val_accuracy: 0.8550
Epoch 108/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3414 - accuracy: 0.8794 - val_loss: 0.3543 - val_accuracy: 0.8467
Epoch 109/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3405 - accuracy: 0.8798 - val_loss: 0.3526 - val_accuracy: 0.8533
Epoch 110/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3414 - accuracy: 0.8797 - val_loss: 0.3543 - val_accuracy: 0.8483
Epoch 111/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3400 - accuracy: 0.8797 - val_loss: 0.3533 - val_accuracy: 0.8517
Epoch 112/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3379 - accuracy: 0.8805 - val_loss: 0.3552 - val_accuracy: 0.8533
Epoch 113/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3375 - accuracy: 0.8809 - val_loss: 0.3574 - val_accuracy: 0.8533
Epoch 114/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3399 - accuracy: 0.8790 - val_loss: 0.3517 - val_accuracy: 0.8550
Epoch 115/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3369 - accuracy: 0.8805 - val_loss: 0.3508 - val_accuracy: 0.8583
Epoch 116/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3371 - accuracy: 0.8808 - val_loss: 0.3524 - val_accuracy: 0.8533
Epoch 117/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3347 - accuracy: 0.8813 - val_loss: 0.3503 - val_accuracy: 0.8500
Epoch 118/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3349 - accuracy: 0.8811 - val_loss: 0.3475 - val_accuracy: 0.8517
Epoch 119/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3335 - accuracy: 0.8820 - val_loss: 0.3498 - val_accuracy: 0.8517
Epoch 120/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3327 - accuracy: 0.8825 - val_loss: 0.3527 - val_accuracy: 0.8567
Epoch 121/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3320 - accuracy: 0.8834 - val_loss: 0.3501 - val_accuracy: 0.8567
Epoch 122/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3321 - accuracy: 0.8826 - val_loss: 0.3531 - val_accuracy: 0.8550
Epoch 123/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3318 - accuracy: 0.8824 - val_loss: 0.3479 - val_accuracy: 0.8533
Epoch 124/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3311 - accuracy: 0.8824 - val_loss: 0.3496 - val_accuracy: 0.8583
Epoch 125/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3293 - accuracy: 0.8831 - val_loss: 0.3545 - val_accuracy: 0.8550
Epoch 126/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3290 - accuracy: 0.8835 - val_loss: 0.3524 - val_accuracy: 0.8533
Epoch 127/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3283 - accuracy: 0.8837 - val_loss: 0.3505 - val_accuracy: 0.8583
Epoch 128/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3272 - accuracy: 0.8839 - val_loss: 0.3498 - val_accuracy: 0.8583
Epoch 129/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3272 - accuracy: 0.8844 - val_loss: 0.3493 - val_accuracy: 0.8550
Epoch 130/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3264 - accuracy: 0.8839 - val_loss: 0.3470 - val_accuracy: 0.8583
Epoch 131/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3256 - accuracy: 0.8845 - val_loss: 0.3463 - val_accuracy: 0.8583
Epoch 132/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3251 - accuracy: 0.8844 - val_loss: 0.3508 - val_accuracy: 0.8567
Epoch 133/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3260 - accuracy: 0.8839 - val_loss: 0.3498 - val_accuracy: 0.8617
Epoch 134/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3241 - accuracy: 0.8850 - val_loss: 0.3430 - val_accuracy: 0.8600
Epoch 135/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3235 - accuracy: 0.8855 - val_loss: 0.3427 - val_accuracy: 0.8600
Epoch 136/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3233 - accuracy: 0.8852 - val_loss: 0.3445 - val_accuracy: 0.8650
Epoch 137/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3215 - accuracy: 0.8857 - val_loss: 0.3410 - val_accuracy: 0.8600
Epoch 138/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3216 - accuracy: 0.8857 - val_loss: 0.3469 - val_accuracy: 0.8633
Epoch 139/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3208 - accuracy: 0.8859 - val_loss: 0.3421 - val_accuracy: 0.8583
Epoch 140/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3204 - accuracy: 0.8858 - val_loss: 0.3437 - val_accuracy: 0.8583
Epoch 141/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3201 - accuracy: 0.8862 - val_loss: 0.3454 - val_accuracy: 0.8633
Epoch 142/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3190 - accuracy: 0.8865 - val_loss: 0.3467 - val_accuracy: 0.8617
Epoch 143/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3192 - accuracy: 0.8865 - val_loss: 0.3463 - val_accuracy: 0.8667
Epoch 144/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3196 - accuracy: 0.8865 - val_loss: 0.3384 - val_accuracy: 0.8667
Epoch 145/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3172 - accuracy: 0.8873 - val_loss: 0.3429 - val_accuracy: 0.8683
Epoch 146/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3168 - accuracy: 0.8885 - val_loss: 0.3391 - val_accuracy: 0.8583
Epoch 147/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3158 - accuracy: 0.8880 - val_loss: 0.3397 - val_accuracy: 0.8617
Epoch 148/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3147 - accuracy: 0.8887 - val_loss: 0.3447 - val_accuracy: 0.8617
Epoch 149/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3145 - accuracy: 0.8885 - val_loss: 0.3387 - val_accuracy: 0.8633
Epoch 150/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3140 - accuracy: 0.8889 - val_loss: 0.3411 - val_accuracy: 0.8633
Epoch 151/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3132 - accuracy: 0.8884 - val_loss: 0.3403 - val_accuracy: 0.8667
Epoch 152/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3125 - accuracy: 0.8894 - val_loss: 0.3358 - val_accuracy: 0.8617
Epoch 153/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3122 - accuracy: 0.8892 - val_loss: 0.3364 - val_accuracy: 0.8667
Epoch 154/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3114 - accuracy: 0.8899 - val_loss: 0.3369 - val_accuracy: 0.8683
Epoch 155/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3114 - accuracy: 0.8893 - val_loss: 0.3444 - val_accuracy: 0.8683
Epoch 156/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3112 - accuracy: 0.8894 - val_loss: 0.3356 - val_accuracy: 0.8667
Epoch 157/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3100 - accuracy: 0.8895 - val_loss: 0.3314 - val_accuracy: 0.8650
Epoch 158/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3097 - accuracy: 0.8901 - val_loss: 0.3373 - val_accuracy: 0.8650
Epoch 159/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3094 - accuracy: 0.8899 - val_loss: 0.3380 - val_accuracy: 0.8633
Epoch 160/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3099 - accuracy: 0.8893 - val_loss: 0.3372 - val_accuracy: 0.8633
Epoch 161/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3090 - accuracy: 0.8902 - val_loss: 0.3355 - val_accuracy: 0.8633
Epoch 162/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3077 - accuracy: 0.8906 - val_loss: 0.3374 - val_accuracy: 0.8567
Epoch 163/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3084 - accuracy: 0.8902 - val_loss: 0.3312 - val_accuracy: 0.8667
Epoch 164/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3075 - accuracy: 0.8908 - val_loss: 0.3356 - val_accuracy: 0.8717
Epoch 165/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3059 - accuracy: 0.8901 - val_loss: 0.3358 - val_accuracy: 0.8683
Epoch 166/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3060 - accuracy: 0.8913 - val_loss: 0.3341 - val_accuracy: 0.8667
Epoch 167/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3043 - accuracy: 0.8917 - val_loss: 0.3319 - val_accuracy: 0.8617
Epoch 168/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3042 - accuracy: 0.8916 - val_loss: 0.3283 - val_accuracy: 0.8617
Epoch 169/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3039 - accuracy: 0.8924 - val_loss: 0.3327 - val_accuracy: 0.8667
Epoch 170/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3034 - accuracy: 0.8919 - val_loss: 0.3290 - val_accuracy: 0.8733
Epoch 171/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3031 - accuracy: 0.8923 - val_loss: 0.3332 - val_accuracy: 0.8717
Epoch 172/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3019 - accuracy: 0.8930 - val_loss: 0.3301 - val_accuracy: 0.8683
Epoch 173/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3019 - accuracy: 0.8924 - val_loss: 0.3324 - val_accuracy: 0.8650
Epoch 174/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3011 - accuracy: 0.8934 - val_loss: 0.3306 - val_accuracy: 0.8667
Epoch 175/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3009 - accuracy: 0.8930 - val_loss: 0.3310 - val_accuracy: 0.8617
Epoch 176/200
117/117 [==============================] - 0s 4ms/step - loss: 0.2996 - accuracy: 0.8929 - val_loss: 0.3307 - val_accuracy: 0.8650
Epoch 177/200
117/117 [==============================] - 0s 3ms/step - loss: 0.2995 - accuracy: 0.8933 - val_loss: 0.3284 - val_accuracy: 0.8650
Epoch 178/200
117/117 [==============================] - 0s 3ms/step - loss: 0.2993 - accuracy: 0.8935 - val_loss: 0.3299 - val_accuracy: 0.8633
Epoch 179/200
117/117 [==============================] - 0s 4ms/step - loss: 0.2994 - accuracy: 0.8937 - val_loss: 0.3336 - val_accuracy: 0.8700
Epoch 180/200
117/117 [==============================] - 0s 4ms/step - loss: 0.2975 - accuracy: 0.8942 - val_loss: 0.3276 - val_accuracy: 0.8650
Epoch 181/200
117/117 [==============================] - 0s 4ms/step - loss: 0.2981 - accuracy: 0.8940 - val_loss: 0.3343 - val_accuracy: 0.8683
Epoch 182/200
117/117 [==============================] - 0s 4ms/step - loss: 0.2969 - accuracy: 0.8949 - val_loss: 0.3326 - val_accuracy: 0.8683
Epoch 183/200
117/117 [==============================] - 0s 4ms/step - loss: 0.2970 - accuracy: 0.8946 - val_loss: 0.3276 - val_accuracy: 0.8600
Epoch 184/200
117/117 [==============================] - 0s 4ms/step - loss: 0.2963 - accuracy: 0.8944 - val_loss: 0.3316 - val_accuracy: 0.8750
Epoch 185/200
117/117 [==============================] - 0s 4ms/step - loss: 0.2952 - accuracy: 0.8941 - val_loss: 0.3219 - val_accuracy: 0.8700
Epoch 186/200
117/117 [==============================] - 0s 4ms/step - loss: 0.2958 - accuracy: 0.8951 - val_loss: 0.3301 - val_accuracy: 0.8650
Epoch 187/200
117/117 [==============================] - 0s 4ms/step - loss: 0.2956 - accuracy: 0.8948 - val_loss: 0.3262 - val_accuracy: 0.8700
Epoch 188/200
117/117 [==============================] - 0s 4ms/step - loss: 0.2939 - accuracy: 0.8950 - val_loss: 0.3255 - val_accuracy: 0.8667
Epoch 189/200
117/117 [==============================] - 0s 3ms/step - loss: 0.2932 - accuracy: 0.8961 - val_loss: 0.3340 - val_accuracy: 0.8667
Epoch 190/200
117/117 [==============================] - 0s 3ms/step - loss: 0.2948 - accuracy: 0.8954 - val_loss: 0.3298 - val_accuracy: 0.8667
Epoch 191/200
117/117 [==============================] - 0s 3ms/step - loss: 0.2950 - accuracy: 0.8945 - val_loss: 0.3254 - val_accuracy: 0.8600
Epoch 192/200
117/117 [==============================] - 0s 3ms/step - loss: 0.2919 - accuracy: 0.8964 - val_loss: 0.3252 - val_accuracy: 0.8650
Epoch 193/200
117/117 [==============================] - 0s 4ms/step - loss: 0.2915 - accuracy: 0.8963 - val_loss: 0.3253 - val_accuracy: 0.8700
Epoch 194/200
117/117 [==============================] - 0s 3ms/step - loss: 0.2908 - accuracy: 0.8963 - val_loss: 0.3237 - val_accuracy: 0.8700
Epoch 195/200
117/117 [==============================] - 0s 2ms/step - loss: 0.2913 - accuracy: 0.8959 - val_loss: 0.3282 - val_accuracy: 0.8667
Epoch 196/200
117/117 [==============================] - 0s 2ms/step - loss: 0.2914 - accuracy: 0.8960 - val_loss: 0.3261 - val_accuracy: 0.8683
Epoch 197/200
117/117 [==============================] - 0s 2ms/step - loss: 0.2895 - accuracy: 0.8966 - val_loss: 0.3250 - val_accuracy: 0.8750
Epoch 198/200
117/117 [==============================] - 0s 2ms/step - loss: 0.2899 - accuracy: 0.8969 - val_loss: 0.3268 - val_accuracy: 0.8717
Epoch 199/200
117/117 [==============================] - 0s 2ms/step - loss: 0.2881 - accuracy: 0.8974 - val_loss: 0.3265 - val_accuracy: 0.8700
Epoch 200/200
117/117 [==============================] - 0s 3ms/step - loss: 0.2900 - accuracy: 0.8965 - val_loss: 0.3265 - val_accuracy: 0.8633# loss 값을 plot 해보겠습니다.
y_vloss = history.history['val_loss']
y_loss = history.history['loss']
x_len = np.arange(len(y_loss))
plt.plot(x_len, y_vloss, marker='.', c='red', label="Validation-set Loss")
plt.plot(x_len, y_loss, marker='.', c='blue', label="Train-set Loss")
plt.legend(loc='upper right')
plt.grid()
plt.title('Loss graph without dropout layer')
plt.ylim(0,1)
plt.xlabel('epoch')
plt.ylabel('loss')
plt.show()
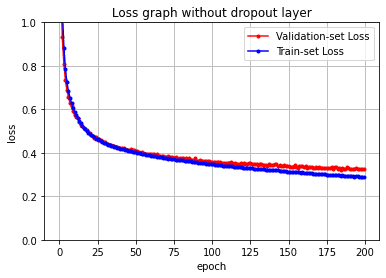
# accuracy 값을 plot 해보겠습니다.
y_vacc = history.history['val_accuracy']
y_acc = history.history['accuracy']
x_len = np.arange(len(y_acc))
plt.plot(x_len, y_vacc, marker='.', c='red', label="Validation-set accuracy")
plt.plot(x_len, y_acc, marker='.', c='blue', label="Train-set accuracy")
plt.legend(loc='lower right')
plt.grid()
plt.ylim(0.5,1)
plt.title('Accuracy graph without dropout layer')
plt.xlabel('epoch')
plt.ylabel('accuracy')
plt.show()
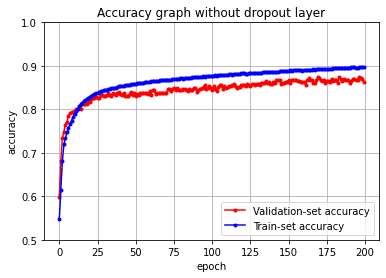
이렇게 200번 epochs 하면 어느순간(loss 한 100부터 accuracy 한 25부터,,)부터 train loss 는 계속 떨어지지만 val loss 는 더이상 움직이지 않는다…
ㅜㅜ 넘해
이럴때 드랍아웃으로 오버피팅 방지
model = keras.Sequential([
keras.layers.Flatten(input_shape=(28, 28)),
keras.layers.Dense(256, activation='relu'),
# 여기에 dropout layer를 추가해보았습니다. 나머지 layer는 위의 실습과 같습니다.
keras.layers.Dropout(0.5),
keras.layers.Dense(10, activation='softmax')
])
model.compile(optimizer='adam',loss='sparse_categorical_crossentropy',
metrics=['accuracy'])
history= model.fit(X_train, y_train, epochs=200, batch_size=512, validation_data=(X_valid, y_valid))Epoch 1/200
117/117 [==============================] - 1s 7ms/step - loss: 2.0802 - accuracy: 0.4763 - val_loss: 1.7029 - val_accuracy: 0.5300
Epoch 2/200
117/117 [==============================] - 0s 3ms/step - loss: 1.4692 - accuracy: 0.5660 - val_loss: 1.2217 - val_accuracy: 0.6350
Epoch 3/200
117/117 [==============================] - 0s 4ms/step - loss: 1.1566 - accuracy: 0.6223 - val_loss: 1.0075 - val_accuracy: 0.7083
Epoch 4/200
117/117 [==============================] - 0s 3ms/step - loss: 0.9942 - accuracy: 0.6671 - val_loss: 0.8747 - val_accuracy: 0.7533
Epoch 5/200
117/117 [==============================] - 0s 3ms/step - loss: 0.8909 - accuracy: 0.6978 - val_loss: 0.7917 - val_accuracy: 0.7600
Epoch 6/200
117/117 [==============================] - 0s 4ms/step - loss: 0.8228 - accuracy: 0.7125 - val_loss: 0.7359 - val_accuracy: 0.7567
Epoch 7/200
117/117 [==============================] - 0s 4ms/step - loss: 0.7727 - accuracy: 0.7269 - val_loss: 0.6952 - val_accuracy: 0.7767
Epoch 8/200
117/117 [==============================] - 0s 4ms/step - loss: 0.7379 - accuracy: 0.7364 - val_loss: 0.6664 - val_accuracy: 0.7833
Epoch 9/200
117/117 [==============================] - 0s 4ms/step - loss: 0.7098 - accuracy: 0.7456 - val_loss: 0.6425 - val_accuracy: 0.7917
Epoch 10/200
117/117 [==============================] - 0s 4ms/step - loss: 0.6862 - accuracy: 0.7520 - val_loss: 0.6225 - val_accuracy: 0.7917
Epoch 11/200
117/117 [==============================] - 0s 4ms/step - loss: 0.6682 - accuracy: 0.7576 - val_loss: 0.6038 - val_accuracy: 0.7967
Epoch 12/200
117/117 [==============================] - 0s 4ms/step - loss: 0.6491 - accuracy: 0.7655 - val_loss: 0.5924 - val_accuracy: 0.7967
Epoch 13/200
117/117 [==============================] - 0s 4ms/step - loss: 0.6348 - accuracy: 0.7712 - val_loss: 0.5801 - val_accuracy: 0.7933
Epoch 14/200
117/117 [==============================] - 0s 4ms/step - loss: 0.6212 - accuracy: 0.7761 - val_loss: 0.5685 - val_accuracy: 0.7950
Epoch 15/200
117/117 [==============================] - 0s 3ms/step - loss: 0.6077 - accuracy: 0.7821 - val_loss: 0.5560 - val_accuracy: 0.7967
Epoch 16/200
117/117 [==============================] - 0s 4ms/step - loss: 0.5986 - accuracy: 0.7863 - val_loss: 0.5497 - val_accuracy: 0.8050
Epoch 17/200
117/117 [==============================] - 0s 4ms/step - loss: 0.5861 - accuracy: 0.7915 - val_loss: 0.5371 - val_accuracy: 0.8017
Epoch 18/200
117/117 [==============================] - 0s 4ms/step - loss: 0.5760 - accuracy: 0.7923 - val_loss: 0.5313 - val_accuracy: 0.8033
Epoch 19/200
117/117 [==============================] - 0s 4ms/step - loss: 0.5669 - accuracy: 0.7980 - val_loss: 0.5252 - val_accuracy: 0.7983
Epoch 20/200
117/117 [==============================] - 0s 4ms/step - loss: 0.5606 - accuracy: 0.7998 - val_loss: 0.5152 - val_accuracy: 0.8067
Epoch 21/200
117/117 [==============================] - 0s 4ms/step - loss: 0.5500 - accuracy: 0.8034 - val_loss: 0.5098 - val_accuracy: 0.8117
Epoch 22/200
117/117 [==============================] - 0s 3ms/step - loss: 0.5430 - accuracy: 0.8059 - val_loss: 0.5044 - val_accuracy: 0.8133
Epoch 23/200
117/117 [==============================] - 0s 4ms/step - loss: 0.5370 - accuracy: 0.8086 - val_loss: 0.4973 - val_accuracy: 0.8117
Epoch 24/200
117/117 [==============================] - 0s 4ms/step - loss: 0.5300 - accuracy: 0.8109 - val_loss: 0.4926 - val_accuracy: 0.8133
Epoch 25/200
117/117 [==============================] - 0s 4ms/step - loss: 0.5257 - accuracy: 0.8133 - val_loss: 0.4880 - val_accuracy: 0.8167
Epoch 26/200
117/117 [==============================] - 0s 4ms/step - loss: 0.5208 - accuracy: 0.8151 - val_loss: 0.4803 - val_accuracy: 0.8217
Epoch 27/200
117/117 [==============================] - 0s 4ms/step - loss: 0.5144 - accuracy: 0.8182 - val_loss: 0.4767 - val_accuracy: 0.8183
Epoch 28/200
117/117 [==============================] - 0s 4ms/step - loss: 0.5101 - accuracy: 0.8194 - val_loss: 0.4730 - val_accuracy: 0.8200
Epoch 29/200
117/117 [==============================] - 0s 3ms/step - loss: 0.5047 - accuracy: 0.8202 - val_loss: 0.4692 - val_accuracy: 0.8267
Epoch 30/200
117/117 [==============================] - 0s 4ms/step - loss: 0.5016 - accuracy: 0.8223 - val_loss: 0.4649 - val_accuracy: 0.8250
Epoch 31/200
117/117 [==============================] - 0s 4ms/step - loss: 0.4949 - accuracy: 0.8246 - val_loss: 0.4627 - val_accuracy: 0.8217
Epoch 32/200
117/117 [==============================] - 0s 4ms/step - loss: 0.4908 - accuracy: 0.8260 - val_loss: 0.4581 - val_accuracy: 0.8200
Epoch 33/200
117/117 [==============================] - 0s 4ms/step - loss: 0.4880 - accuracy: 0.8282 - val_loss: 0.4540 - val_accuracy: 0.8267
Epoch 34/200
117/117 [==============================] - 0s 4ms/step - loss: 0.4853 - accuracy: 0.8270 - val_loss: 0.4477 - val_accuracy: 0.8250
Epoch 35/200
117/117 [==============================] - 0s 4ms/step - loss: 0.4800 - accuracy: 0.8301 - val_loss: 0.4479 - val_accuracy: 0.8267
Epoch 36/200
117/117 [==============================] - 0s 4ms/step - loss: 0.4784 - accuracy: 0.8317 - val_loss: 0.4423 - val_accuracy: 0.8317
Epoch 37/200
117/117 [==============================] - 0s 4ms/step - loss: 0.4746 - accuracy: 0.8326 - val_loss: 0.4429 - val_accuracy: 0.8283
Epoch 38/200
117/117 [==============================] - 0s 4ms/step - loss: 0.4712 - accuracy: 0.8336 - val_loss: 0.4392 - val_accuracy: 0.8350
Epoch 39/200
117/117 [==============================] - 0s 4ms/step - loss: 0.4680 - accuracy: 0.8346 - val_loss: 0.4364 - val_accuracy: 0.8333
Epoch 40/200
117/117 [==============================] - 0s 4ms/step - loss: 0.4642 - accuracy: 0.8361 - val_loss: 0.4352 - val_accuracy: 0.8333
Epoch 41/200
117/117 [==============================] - 0s 4ms/step - loss: 0.4625 - accuracy: 0.8360 - val_loss: 0.4318 - val_accuracy: 0.8367
Epoch 42/200
117/117 [==============================] - 0s 4ms/step - loss: 0.4589 - accuracy: 0.8378 - val_loss: 0.4305 - val_accuracy: 0.8317
Epoch 43/200
117/117 [==============================] - 0s 4ms/step - loss: 0.4571 - accuracy: 0.8379 - val_loss: 0.4267 - val_accuracy: 0.8317
Epoch 44/200
117/117 [==============================] - 0s 3ms/step - loss: 0.4558 - accuracy: 0.8400 - val_loss: 0.4250 - val_accuracy: 0.8317
Epoch 45/200
117/117 [==============================] - 0s 3ms/step - loss: 0.4527 - accuracy: 0.8407 - val_loss: 0.4234 - val_accuracy: 0.8350
Epoch 46/200
117/117 [==============================] - 0s 4ms/step - loss: 0.4514 - accuracy: 0.8398 - val_loss: 0.4185 - val_accuracy: 0.8350
Epoch 47/200
117/117 [==============================] - 0s 4ms/step - loss: 0.4457 - accuracy: 0.8415 - val_loss: 0.4165 - val_accuracy: 0.8333
Epoch 48/200
117/117 [==============================] - 0s 3ms/step - loss: 0.4460 - accuracy: 0.8418 - val_loss: 0.4174 - val_accuracy: 0.8367
Epoch 49/200
117/117 [==============================] - 0s 4ms/step - loss: 0.4429 - accuracy: 0.8442 - val_loss: 0.4194 - val_accuracy: 0.8317
Epoch 50/200
117/117 [==============================] - 0s 3ms/step - loss: 0.4414 - accuracy: 0.8431 - val_loss: 0.4114 - val_accuracy: 0.8383
Epoch 51/200
117/117 [==============================] - 0s 4ms/step - loss: 0.4384 - accuracy: 0.8454 - val_loss: 0.4127 - val_accuracy: 0.8350
Epoch 52/200
117/117 [==============================] - 0s 4ms/step - loss: 0.4373 - accuracy: 0.8446 - val_loss: 0.4082 - val_accuracy: 0.8400
Epoch 53/200
117/117 [==============================] - 0s 3ms/step - loss: 0.4359 - accuracy: 0.8454 - val_loss: 0.4059 - val_accuracy: 0.8383
Epoch 54/200
117/117 [==============================] - 0s 4ms/step - loss: 0.4325 - accuracy: 0.8479 - val_loss: 0.4040 - val_accuracy: 0.8367
Epoch 55/200
117/117 [==============================] - 0s 4ms/step - loss: 0.4301 - accuracy: 0.8481 - val_loss: 0.4016 - val_accuracy: 0.8367
Epoch 56/200
117/117 [==============================] - 0s 4ms/step - loss: 0.4268 - accuracy: 0.8489 - val_loss: 0.4070 - val_accuracy: 0.8400
Epoch 57/200
117/117 [==============================] - 0s 3ms/step - loss: 0.4268 - accuracy: 0.8487 - val_loss: 0.4012 - val_accuracy: 0.8367
Epoch 58/200
117/117 [==============================] - 0s 4ms/step - loss: 0.4239 - accuracy: 0.8498 - val_loss: 0.3998 - val_accuracy: 0.8383
Epoch 59/200
117/117 [==============================] - 0s 3ms/step - loss: 0.4242 - accuracy: 0.8508 - val_loss: 0.3976 - val_accuracy: 0.8333
Epoch 60/200
117/117 [==============================] - 0s 4ms/step - loss: 0.4232 - accuracy: 0.8501 - val_loss: 0.3967 - val_accuracy: 0.8383
Epoch 61/200
117/117 [==============================] - 0s 4ms/step - loss: 0.4207 - accuracy: 0.8499 - val_loss: 0.3960 - val_accuracy: 0.8350
Epoch 62/200
117/117 [==============================] - 0s 3ms/step - loss: 0.4190 - accuracy: 0.8510 - val_loss: 0.3976 - val_accuracy: 0.8367
Epoch 63/200
117/117 [==============================] - 0s 4ms/step - loss: 0.4183 - accuracy: 0.8520 - val_loss: 0.3940 - val_accuracy: 0.8400
Epoch 64/200
117/117 [==============================] - 0s 3ms/step - loss: 0.4154 - accuracy: 0.8527 - val_loss: 0.3922 - val_accuracy: 0.8350
Epoch 65/200
117/117 [==============================] - 0s 4ms/step - loss: 0.4156 - accuracy: 0.8531 - val_loss: 0.3937 - val_accuracy: 0.8383
Epoch 66/200
117/117 [==============================] - 0s 4ms/step - loss: 0.4129 - accuracy: 0.8537 - val_loss: 0.3896 - val_accuracy: 0.8400
Epoch 67/200
117/117 [==============================] - 0s 4ms/step - loss: 0.4136 - accuracy: 0.8532 - val_loss: 0.3890 - val_accuracy: 0.8417
Epoch 68/200
117/117 [==============================] - 0s 3ms/step - loss: 0.4104 - accuracy: 0.8547 - val_loss: 0.3869 - val_accuracy: 0.8383
Epoch 69/200
117/117 [==============================] - 0s 4ms/step - loss: 0.4077 - accuracy: 0.8564 - val_loss: 0.3861 - val_accuracy: 0.8467
Epoch 70/200
117/117 [==============================] - 0s 4ms/step - loss: 0.4075 - accuracy: 0.8553 - val_loss: 0.3848 - val_accuracy: 0.8417
Epoch 71/200
117/117 [==============================] - 0s 4ms/step - loss: 0.4047 - accuracy: 0.8579 - val_loss: 0.3820 - val_accuracy: 0.8433
Epoch 72/200
117/117 [==============================] - 0s 4ms/step - loss: 0.4054 - accuracy: 0.8558 - val_loss: 0.3827 - val_accuracy: 0.8400
Epoch 73/200
117/117 [==============================] - 0s 3ms/step - loss: 0.4042 - accuracy: 0.8575 - val_loss: 0.3828 - val_accuracy: 0.8400
Epoch 74/200
117/117 [==============================] - 0s 3ms/step - loss: 0.4020 - accuracy: 0.8579 - val_loss: 0.3800 - val_accuracy: 0.8433
Epoch 75/200
117/117 [==============================] - 0s 4ms/step - loss: 0.4001 - accuracy: 0.8583 - val_loss: 0.3794 - val_accuracy: 0.8450
Epoch 76/200
117/117 [==============================] - 0s 4ms/step - loss: 0.4005 - accuracy: 0.8568 - val_loss: 0.3768 - val_accuracy: 0.8450
Epoch 77/200
117/117 [==============================] - 0s 4ms/step - loss: 0.4001 - accuracy: 0.8576 - val_loss: 0.3765 - val_accuracy: 0.8467
Epoch 78/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3980 - accuracy: 0.8592 - val_loss: 0.3773 - val_accuracy: 0.8467
Epoch 79/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3976 - accuracy: 0.8593 - val_loss: 0.3762 - val_accuracy: 0.8517
Epoch 80/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3961 - accuracy: 0.8594 - val_loss: 0.3729 - val_accuracy: 0.8450
Epoch 81/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3945 - accuracy: 0.8586 - val_loss: 0.3714 - val_accuracy: 0.8433
Epoch 82/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3916 - accuracy: 0.8619 - val_loss: 0.3736 - val_accuracy: 0.8467
Epoch 83/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3925 - accuracy: 0.8623 - val_loss: 0.3728 - val_accuracy: 0.8433
Epoch 84/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3913 - accuracy: 0.8614 - val_loss: 0.3716 - val_accuracy: 0.8483
Epoch 85/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3890 - accuracy: 0.8621 - val_loss: 0.3704 - val_accuracy: 0.8433
Epoch 86/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3872 - accuracy: 0.8621 - val_loss: 0.3699 - val_accuracy: 0.8450
Epoch 87/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3875 - accuracy: 0.8614 - val_loss: 0.3710 - val_accuracy: 0.8483
Epoch 88/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3863 - accuracy: 0.8630 - val_loss: 0.3666 - val_accuracy: 0.8417
Epoch 89/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3847 - accuracy: 0.8626 - val_loss: 0.3684 - val_accuracy: 0.8467
Epoch 90/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3837 - accuracy: 0.8634 - val_loss: 0.3681 - val_accuracy: 0.8450
Epoch 91/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3835 - accuracy: 0.8646 - val_loss: 0.3655 - val_accuracy: 0.8517
Epoch 92/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3840 - accuracy: 0.8640 - val_loss: 0.3673 - val_accuracy: 0.8467
Epoch 93/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3825 - accuracy: 0.8646 - val_loss: 0.3628 - val_accuracy: 0.8500
Epoch 94/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3796 - accuracy: 0.8639 - val_loss: 0.3630 - val_accuracy: 0.8450
Epoch 95/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3789 - accuracy: 0.8657 - val_loss: 0.3628 - val_accuracy: 0.8517
Epoch 96/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3788 - accuracy: 0.8660 - val_loss: 0.3638 - val_accuracy: 0.8517
Epoch 97/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3784 - accuracy: 0.8671 - val_loss: 0.3629 - val_accuracy: 0.8533
Epoch 98/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3768 - accuracy: 0.8661 - val_loss: 0.3609 - val_accuracy: 0.8567
Epoch 99/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3752 - accuracy: 0.8662 - val_loss: 0.3623 - val_accuracy: 0.8550
Epoch 100/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3743 - accuracy: 0.8666 - val_loss: 0.3586 - val_accuracy: 0.8550
Epoch 101/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3751 - accuracy: 0.8674 - val_loss: 0.3573 - val_accuracy: 0.8417
Epoch 102/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3748 - accuracy: 0.8675 - val_loss: 0.3605 - val_accuracy: 0.8550
Epoch 103/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3722 - accuracy: 0.8695 - val_loss: 0.3577 - val_accuracy: 0.8533
Epoch 104/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3718 - accuracy: 0.8669 - val_loss: 0.3558 - val_accuracy: 0.8517
Epoch 105/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3714 - accuracy: 0.8672 - val_loss: 0.3577 - val_accuracy: 0.8550
Epoch 106/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3703 - accuracy: 0.8689 - val_loss: 0.3540 - val_accuracy: 0.8533
Epoch 107/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3681 - accuracy: 0.8686 - val_loss: 0.3565 - val_accuracy: 0.8533
Epoch 108/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3705 - accuracy: 0.8687 - val_loss: 0.3529 - val_accuracy: 0.8500
Epoch 109/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3668 - accuracy: 0.8696 - val_loss: 0.3523 - val_accuracy: 0.8533
Epoch 110/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3671 - accuracy: 0.8700 - val_loss: 0.3537 - val_accuracy: 0.8550
Epoch 111/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3668 - accuracy: 0.8699 - val_loss: 0.3520 - val_accuracy: 0.8550
Epoch 112/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3648 - accuracy: 0.8715 - val_loss: 0.3499 - val_accuracy: 0.8583
Epoch 113/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3622 - accuracy: 0.8721 - val_loss: 0.3496 - val_accuracy: 0.8600
Epoch 114/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3636 - accuracy: 0.8721 - val_loss: 0.3508 - val_accuracy: 0.8467
Epoch 115/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3637 - accuracy: 0.8709 - val_loss: 0.3480 - val_accuracy: 0.8550
Epoch 116/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3616 - accuracy: 0.8717 - val_loss: 0.3514 - val_accuracy: 0.8583
Epoch 117/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3602 - accuracy: 0.8720 - val_loss: 0.3462 - val_accuracy: 0.8533
Epoch 118/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3616 - accuracy: 0.8716 - val_loss: 0.3518 - val_accuracy: 0.8567
Epoch 119/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3597 - accuracy: 0.8719 - val_loss: 0.3479 - val_accuracy: 0.8583
Epoch 120/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3584 - accuracy: 0.8726 - val_loss: 0.3491 - val_accuracy: 0.8583
Epoch 121/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3588 - accuracy: 0.8727 - val_loss: 0.3466 - val_accuracy: 0.8583
Epoch 122/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3576 - accuracy: 0.8732 - val_loss: 0.3459 - val_accuracy: 0.8517
Epoch 123/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3544 - accuracy: 0.8743 - val_loss: 0.3451 - val_accuracy: 0.8583
Epoch 124/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3557 - accuracy: 0.8739 - val_loss: 0.3430 - val_accuracy: 0.8550
Epoch 125/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3555 - accuracy: 0.8745 - val_loss: 0.3430 - val_accuracy: 0.8600
Epoch 126/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3546 - accuracy: 0.8729 - val_loss: 0.3442 - val_accuracy: 0.8583
Epoch 127/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3545 - accuracy: 0.8746 - val_loss: 0.3435 - val_accuracy: 0.8600
Epoch 128/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3551 - accuracy: 0.8736 - val_loss: 0.3405 - val_accuracy: 0.8550
Epoch 129/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3532 - accuracy: 0.8750 - val_loss: 0.3415 - val_accuracy: 0.8567
Epoch 130/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3521 - accuracy: 0.8753 - val_loss: 0.3397 - val_accuracy: 0.8583
Epoch 131/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3499 - accuracy: 0.8756 - val_loss: 0.3405 - val_accuracy: 0.8550
Epoch 132/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3513 - accuracy: 0.8753 - val_loss: 0.3395 - val_accuracy: 0.8617
Epoch 133/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3489 - accuracy: 0.8758 - val_loss: 0.3397 - val_accuracy: 0.8600
Epoch 134/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3509 - accuracy: 0.8758 - val_loss: 0.3412 - val_accuracy: 0.8567
Epoch 135/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3483 - accuracy: 0.8770 - val_loss: 0.3386 - val_accuracy: 0.8583
Epoch 136/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3483 - accuracy: 0.8758 - val_loss: 0.3384 - val_accuracy: 0.8583
Epoch 137/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3462 - accuracy: 0.8777 - val_loss: 0.3378 - val_accuracy: 0.8583
Epoch 138/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3465 - accuracy: 0.8774 - val_loss: 0.3392 - val_accuracy: 0.8617
Epoch 139/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3469 - accuracy: 0.8769 - val_loss: 0.3361 - val_accuracy: 0.8583
Epoch 140/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3464 - accuracy: 0.8778 - val_loss: 0.3370 - val_accuracy: 0.8567
Epoch 141/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3433 - accuracy: 0.8785 - val_loss: 0.3343 - val_accuracy: 0.8600
Epoch 142/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3455 - accuracy: 0.8782 - val_loss: 0.3373 - val_accuracy: 0.8600
Epoch 143/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3445 - accuracy: 0.8778 - val_loss: 0.3357 - val_accuracy: 0.8583
Epoch 144/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3435 - accuracy: 0.8786 - val_loss: 0.3356 - val_accuracy: 0.8617
Epoch 145/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3420 - accuracy: 0.8781 - val_loss: 0.3364 - val_accuracy: 0.8650
Epoch 146/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3446 - accuracy: 0.8782 - val_loss: 0.3342 - val_accuracy: 0.8600
Epoch 147/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3422 - accuracy: 0.8781 - val_loss: 0.3342 - val_accuracy: 0.8650
Epoch 148/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3424 - accuracy: 0.8787 - val_loss: 0.3343 - val_accuracy: 0.8550
Epoch 149/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3397 - accuracy: 0.8788 - val_loss: 0.3328 - val_accuracy: 0.8600
Epoch 150/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3378 - accuracy: 0.8798 - val_loss: 0.3332 - val_accuracy: 0.8633
Epoch 151/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3398 - accuracy: 0.8788 - val_loss: 0.3333 - val_accuracy: 0.8567
Epoch 152/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3389 - accuracy: 0.8793 - val_loss: 0.3336 - val_accuracy: 0.8650
Epoch 153/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3384 - accuracy: 0.8806 - val_loss: 0.3335 - val_accuracy: 0.8600
Epoch 154/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3365 - accuracy: 0.8803 - val_loss: 0.3319 - val_accuracy: 0.8567
Epoch 155/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3381 - accuracy: 0.8811 - val_loss: 0.3323 - val_accuracy: 0.8617
Epoch 156/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3382 - accuracy: 0.8801 - val_loss: 0.3308 - val_accuracy: 0.8617
Epoch 157/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3364 - accuracy: 0.8808 - val_loss: 0.3269 - val_accuracy: 0.8617
Epoch 158/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3374 - accuracy: 0.8804 - val_loss: 0.3304 - val_accuracy: 0.8683
Epoch 159/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3361 - accuracy: 0.8809 - val_loss: 0.3298 - val_accuracy: 0.8583
Epoch 160/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3343 - accuracy: 0.8813 - val_loss: 0.3296 - val_accuracy: 0.8650
Epoch 161/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3336 - accuracy: 0.8816 - val_loss: 0.3282 - val_accuracy: 0.8700
Epoch 162/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3335 - accuracy: 0.8817 - val_loss: 0.3293 - val_accuracy: 0.8600
Epoch 163/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3334 - accuracy: 0.8810 - val_loss: 0.3317 - val_accuracy: 0.8650
Epoch 164/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3312 - accuracy: 0.8828 - val_loss: 0.3252 - val_accuracy: 0.8633
Epoch 165/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3315 - accuracy: 0.8819 - val_loss: 0.3271 - val_accuracy: 0.8700
Epoch 166/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3320 - accuracy: 0.8823 - val_loss: 0.3270 - val_accuracy: 0.8633
Epoch 167/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3322 - accuracy: 0.8825 - val_loss: 0.3263 - val_accuracy: 0.8650
Epoch 168/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3315 - accuracy: 0.8830 - val_loss: 0.3270 - val_accuracy: 0.8600
Epoch 169/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3307 - accuracy: 0.8824 - val_loss: 0.3241 - val_accuracy: 0.8617
Epoch 170/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3296 - accuracy: 0.8829 - val_loss: 0.3249 - val_accuracy: 0.8650
Epoch 171/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3314 - accuracy: 0.8823 - val_loss: 0.3261 - val_accuracy: 0.8650
Epoch 172/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3277 - accuracy: 0.8836 - val_loss: 0.3255 - val_accuracy: 0.8650
Epoch 173/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3312 - accuracy: 0.8824 - val_loss: 0.3264 - val_accuracy: 0.8633
Epoch 174/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3284 - accuracy: 0.8830 - val_loss: 0.3247 - val_accuracy: 0.8650
Epoch 175/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3266 - accuracy: 0.8836 - val_loss: 0.3226 - val_accuracy: 0.8683
Epoch 176/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3266 - accuracy: 0.8835 - val_loss: 0.3229 - val_accuracy: 0.8633
Epoch 177/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3261 - accuracy: 0.8841 - val_loss: 0.3252 - val_accuracy: 0.8633
Epoch 178/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3229 - accuracy: 0.8872 - val_loss: 0.3233 - val_accuracy: 0.8650
Epoch 179/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3282 - accuracy: 0.8845 - val_loss: 0.3215 - val_accuracy: 0.8667
Epoch 180/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3264 - accuracy: 0.8844 - val_loss: 0.3245 - val_accuracy: 0.8617
Epoch 181/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3247 - accuracy: 0.8846 - val_loss: 0.3210 - val_accuracy: 0.8633
Epoch 182/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3253 - accuracy: 0.8843 - val_loss: 0.3230 - val_accuracy: 0.8667
Epoch 183/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3243 - accuracy: 0.8842 - val_loss: 0.3240 - val_accuracy: 0.8650
Epoch 184/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3248 - accuracy: 0.8845 - val_loss: 0.3199 - val_accuracy: 0.8700
Epoch 185/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3242 - accuracy: 0.8856 - val_loss: 0.3225 - val_accuracy: 0.8733
Epoch 186/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3236 - accuracy: 0.8844 - val_loss: 0.3208 - val_accuracy: 0.8650
Epoch 187/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3223 - accuracy: 0.8859 - val_loss: 0.3167 - val_accuracy: 0.8667
Epoch 188/200
117/117 [==============================] - 0s 4ms/step - loss: 0.3214 - accuracy: 0.8849 - val_loss: 0.3201 - val_accuracy: 0.8633
Epoch 189/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3260 - accuracy: 0.8848 - val_loss: 0.3202 - val_accuracy: 0.8717
Epoch 190/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3214 - accuracy: 0.8855 - val_loss: 0.3192 - val_accuracy: 0.8633
Epoch 191/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3205 - accuracy: 0.8861 - val_loss: 0.3214 - val_accuracy: 0.8650
Epoch 192/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3213 - accuracy: 0.8857 - val_loss: 0.3180 - val_accuracy: 0.8700
Epoch 193/200
117/117 [==============================] - 0s 2ms/step - loss: 0.3203 - accuracy: 0.8859 - val_loss: 0.3191 - val_accuracy: 0.8617
Epoch 194/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3223 - accuracy: 0.8858 - val_loss: 0.3170 - val_accuracy: 0.8683
Epoch 195/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3216 - accuracy: 0.8862 - val_loss: 0.3222 - val_accuracy: 0.8667
Epoch 196/200
117/117 [==============================] - 0s 2ms/step - loss: 0.3196 - accuracy: 0.8860 - val_loss: 0.3167 - val_accuracy: 0.8700
Epoch 197/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3179 - accuracy: 0.8880 - val_loss: 0.3194 - val_accuracy: 0.8700
Epoch 198/200
117/117 [==============================] - 0s 3ms/step - loss: 0.3185 - accuracy: 0.8865 - val_loss: 0.3178 - val_accuracy: 0.8633
Epoch 199/200
117/117 [==============================] - 0s 2ms/step - loss: 0.3152 - accuracy: 0.8877 - val_loss: 0.3137 - val_accuracy: 0.8667
Epoch 200/200
117/117 [==============================] - 0s 2ms/step - loss: 0.3166 - accuracy: 0.8876 - val_loss: 0.3202 - val_accuracy: 0.8650# loss 값을 plot 해보겠습니다.
y_vloss = history.history['val_loss']
y_loss = history.history['loss']
x_len = np.arange(len(y_loss))
plt.plot(x_len, y_vloss, marker='.', c='red', label="Validation-set Loss")
plt.plot(x_len, y_loss, marker='.', c='blue', label="Train-set Loss")
plt.legend(loc='upper right')
plt.grid()
plt.ylim(0,1)
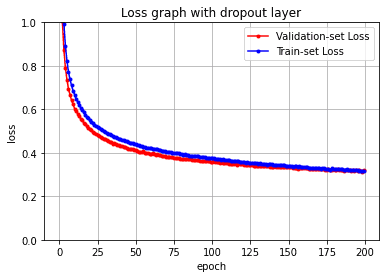
plt.title('Loss graph with dropout layer')
plt.xlabel('epoch')
plt.ylabel('loss')
plt.show()
# accuracy 값을 plot 해보겠습니다.
y_vacc = history.history['val_accuracy']
y_acc = history.history['accuracy']
x_len = np.arange(len(y_acc))
plt.plot(x_len, y_vacc, marker='.', c='red', label="Validation-set accuracy")
plt.plot(x_len, y_acc, marker='.', c='blue', label="Train-set accuracy")
plt.legend(loc='lower right')
plt.grid()
plt.ylim(0.5,1)
plt.title('Accuracy graph with dropout layer')
plt.xlabel('epoch')
plt.ylabel('accuracy')
plt.show()
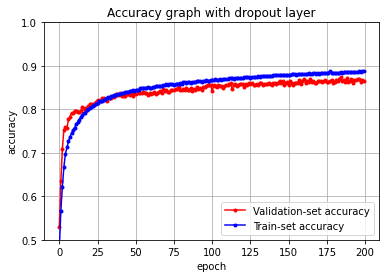
진짜 조금 바뀌긴 했지만 차이가 있긴 있다
사실 더 복잡한 네트워크나, 더 어려운 데이터의 경우에는 이러한 오버피팅이 더 자주 있는 일이므로, Dropout layer를 추가하는 경우가 많습니다. 하지만 이 또한 확률 값이 파라미터로 들어가므로, 어떠한 값을 선택하느냐는 데이터와 네트워크에 따라 달린 일입니다.
Batch Normalization
요건 기울기소실 이랑 기울기포화 문제를 해결한다.
쉽게 말하면 미니배치에서
평균이랑 분산을 구해가지고
x에서 평균뺀거를 분산으로 나눈 값으로 정규화 하는거
특히 중요한 부분은 분모에 엡실론(0.001)) 가 추가된 것이다 이 부분으로
가중치 소실, 포화를 막을 수 있다. 그래서 이걸로 오버피팅으로 학습이 잘되지 않는 것을 막을 수 있닫.
fashion_mnist 데이터로 가져가보자
import tensorflow as tf
from tensorflow import keras
import numpy as np
import matplotlib.pyplot as plt
fashion_mnist = keras.datasets.fashion_mnist
print('=3')=3(train_images, train_labels), (test_images, test_labels) = fashion_mnist.load_data()
class_names = ['T-shirt/top', 'Trouser', 'Pullover', 'Dress', 'Coat',
'Sandal', 'Shirt', 'Sneaker', 'Bag', 'Ankle boot']
train_images = train_images / 255.0
test_images = test_images / 255.0from sklearn.model_selection import train_test_split
X_train, X_valid, y_train, y_valid = train_test_split(train_images, train_labels, test_size=0.3, random_state=101)
model = keras.Sequential([
keras.layers.Flatten(input_shape=(28, 28)),
keras.layers.Dense(128, activation='relu'),
keras.layers.Dense(10, activation='softmax')
])
model.compile(optimizer='adam',loss='sparse_categorical_crossentropy',
metrics=['accuracy'])
history= model.fit(X_train, y_train, epochs=20, batch_size=2048, validation_data=(X_valid, y_valid))Epoch 1/20
21/21 [==============================] - 1s 23ms/step - loss: 1.2103 - accuracy: 0.6096 - val_loss: 0.7485 - val_accuracy: 0.7401
Epoch 2/20
21/21 [==============================] - 0s 10ms/step - loss: 0.6556 - accuracy: 0.7789 - val_loss: 0.5983 - val_accuracy: 0.8006
Epoch 3/20
21/21 [==============================] - 0s 10ms/step - loss: 0.5541 - accuracy: 0.8160 - val_loss: 0.5364 - val_accuracy: 0.8184
Epoch 4/20
21/21 [==============================] - 0s 9ms/step - loss: 0.5061 - accuracy: 0.8299 - val_loss: 0.5008 - val_accuracy: 0.8274
Epoch 5/20
21/21 [==============================] - 0s 9ms/step - loss: 0.4775 - accuracy: 0.8394 - val_loss: 0.4801 - val_accuracy: 0.8369
Epoch 6/20
21/21 [==============================] - 0s 9ms/step - loss: 0.4555 - accuracy: 0.8452 - val_loss: 0.4612 - val_accuracy: 0.8456
Epoch 7/20
21/21 [==============================] - 0s 9ms/step - loss: 0.4391 - accuracy: 0.8502 - val_loss: 0.4470 - val_accuracy: 0.8479
Epoch 8/20
21/21 [==============================] - 0s 8ms/step - loss: 0.4251 - accuracy: 0.8559 - val_loss: 0.4369 - val_accuracy: 0.8503
Epoch 9/20
21/21 [==============================] - 0s 6ms/step - loss: 0.4144 - accuracy: 0.8578 - val_loss: 0.4295 - val_accuracy: 0.8530
Epoch 10/20
21/21 [==============================] - 0s 6ms/step - loss: 0.4059 - accuracy: 0.8595 - val_loss: 0.4182 - val_accuracy: 0.8566
Epoch 11/20
21/21 [==============================] - 0s 7ms/step - loss: 0.3950 - accuracy: 0.8646 - val_loss: 0.4125 - val_accuracy: 0.8588
Epoch 12/20
21/21 [==============================] - 0s 6ms/step - loss: 0.3900 - accuracy: 0.8662 - val_loss: 0.4139 - val_accuracy: 0.8543
Epoch 13/20
21/21 [==============================] - 0s 6ms/step - loss: 0.3826 - accuracy: 0.8678 - val_loss: 0.4036 - val_accuracy: 0.8598
Epoch 14/20
21/21 [==============================] - 0s 6ms/step - loss: 0.3731 - accuracy: 0.8719 - val_loss: 0.3979 - val_accuracy: 0.8619
Epoch 15/20
21/21 [==============================] - 0s 6ms/step - loss: 0.3696 - accuracy: 0.8723 - val_loss: 0.3929 - val_accuracy: 0.8624
Epoch 16/20
21/21 [==============================] - 0s 6ms/step - loss: 0.3614 - accuracy: 0.8761 - val_loss: 0.3878 - val_accuracy: 0.8650
Epoch 17/20
21/21 [==============================] - 0s 6ms/step - loss: 0.3560 - accuracy: 0.8774 - val_loss: 0.3865 - val_accuracy: 0.8647
Epoch 18/20
21/21 [==============================] - 0s 6ms/step - loss: 0.3514 - accuracy: 0.8776 - val_loss: 0.3858 - val_accuracy: 0.8644
Epoch 19/20
21/21 [==============================] - 0s 6ms/step - loss: 0.3476 - accuracy: 0.8803 - val_loss: 0.3774 - val_accuracy: 0.8686
Epoch 20/20
21/21 [==============================] - 0s 6ms/step - loss: 0.3385 - accuracy: 0.8828 - val_loss: 0.3780 - val_accuracy: 0.8672# loss 값을 plot 해보겠습니다.
y_vloss = history.history['val_loss']
y_loss = history.history['loss']
x_len = np.arange(len(y_loss))
plt.plot(x_len, y_vloss, marker='.', c='red', label="Validation-set Loss")
plt.plot(x_len, y_loss, marker='.', c='blue', label="Train-set Loss")
plt.legend(loc='upper right')
plt.grid()
plt.ylim(0,1)
plt.title('Loss graph without batch normalization')
plt.xlabel('epoch')
plt.ylabel('loss')
plt.show()
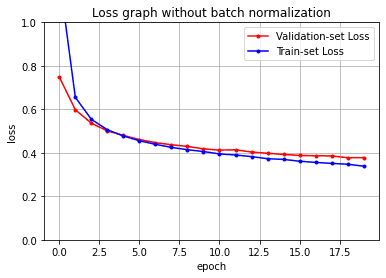
일반적인 Dense FC layer 를 쓰면 저렇게 val loss가 7.5 쯤에서 멈춘다
# accuracy 값을 plot 해보겠습니다.
y_vacc = history.history['val_accuracy']
y_acc = history.history['accuracy']
x_len = np.arange(len(y_acc))
plt.plot(x_len, y_vacc, marker='.', c='red', label="Validation-set accuracy")
plt.plot(x_len, y_acc, marker='.', c='blue', label="Train-set accuracy")
plt.legend(loc='lower right')
plt.grid()
plt.ylim(0.5,1)
plt.title('Accuracy graph without batch normalization')
plt.xlabel('epoch')
plt.ylabel('accuracy')
plt.show()
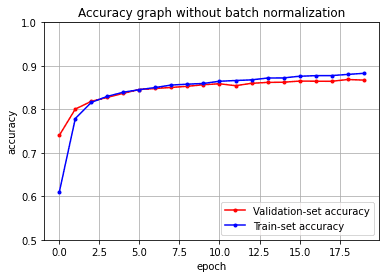
배치 노말라이제이션 쓰면
model = keras.Sequential([
keras.layers.Flatten(input_shape=(28, 28)),
keras.layers.Dense(128, activation='relu'),
#여기에 batchnormalization layer를 추가해보았습니다. 나머지 layer는 위의 실습과 같습니다.
keras.layers.BatchNormalization(),
keras.layers.Dense(10, activation='softmax')
])
model.compile(optimizer='adam',loss='sparse_categorical_crossentropy',
metrics=['accuracy'])
history= model.fit(X_train, y_train, epochs=20, batch_size=2048, validation_data=(X_valid, y_valid))Epoch 1/20
21/21 [==============================] - 1s 25ms/step - loss: 0.8808 - accuracy: 0.7005 - val_loss: 1.0613 - val_accuracy: 0.6525
Epoch 2/20
21/21 [==============================] - 0s 9ms/step - loss: 0.5167 - accuracy: 0.8267 - val_loss: 0.8411 - val_accuracy: 0.7488
Epoch 3/20
21/21 [==============================] - 0s 10ms/step - loss: 0.4500 - accuracy: 0.8469 - val_loss: 0.7390 - val_accuracy: 0.7935
Epoch 4/20
21/21 [==============================] - 0s 9ms/step - loss: 0.4127 - accuracy: 0.8584 - val_loss: 0.6659 - val_accuracy: 0.8183
Epoch 5/20
21/21 [==============================] - 0s 10ms/step - loss: 0.3869 - accuracy: 0.8680 - val_loss: 0.6321 - val_accuracy: 0.8328
Epoch 6/20
21/21 [==============================] - 0s 9ms/step - loss: 0.3640 - accuracy: 0.8746 - val_loss: 0.5769 - val_accuracy: 0.8439
Epoch 7/20
21/21 [==============================] - 0s 10ms/step - loss: 0.3465 - accuracy: 0.8790 - val_loss: 0.5427 - val_accuracy: 0.8486
Epoch 8/20
21/21 [==============================] - 0s 6ms/step - loss: 0.3321 - accuracy: 0.8842 - val_loss: 0.5140 - val_accuracy: 0.8510
Epoch 9/20
21/21 [==============================] - 0s 7ms/step - loss: 0.3164 - accuracy: 0.8903 - val_loss: 0.4943 - val_accuracy: 0.8492
Epoch 10/20
21/21 [==============================] - 0s 7ms/step - loss: 0.3045 - accuracy: 0.8935 - val_loss: 0.4571 - val_accuracy: 0.8611
Epoch 11/20
21/21 [==============================] - 0s 7ms/step - loss: 0.2944 - accuracy: 0.8968 - val_loss: 0.4447 - val_accuracy: 0.8588
Epoch 12/20
21/21 [==============================] - 0s 6ms/step - loss: 0.2839 - accuracy: 0.9001 - val_loss: 0.4193 - val_accuracy: 0.8649
Epoch 13/20
21/21 [==============================] - 0s 7ms/step - loss: 0.2733 - accuracy: 0.9047 - val_loss: 0.4101 - val_accuracy: 0.8683
Epoch 14/20
21/21 [==============================] - 0s 6ms/step - loss: 0.2639 - accuracy: 0.9089 - val_loss: 0.4099 - val_accuracy: 0.8638
Epoch 15/20
21/21 [==============================] - 0s 6ms/step - loss: 0.2580 - accuracy: 0.9097 - val_loss: 0.3807 - val_accuracy: 0.8750
Epoch 16/20
21/21 [==============================] - 0s 6ms/step - loss: 0.2502 - accuracy: 0.9125 - val_loss: 0.3694 - val_accuracy: 0.8753
Epoch 17/20
21/21 [==============================] - 0s 6ms/step - loss: 0.2434 - accuracy: 0.9149 - val_loss: 0.3822 - val_accuracy: 0.8688
Epoch 18/20
21/21 [==============================] - 0s 7ms/step - loss: 0.2365 - accuracy: 0.9167 - val_loss: 0.3545 - val_accuracy: 0.8790
Epoch 19/20
21/21 [==============================] - 0s 6ms/step - loss: 0.2273 - accuracy: 0.9210 - val_loss: 0.3586 - val_accuracy: 0.8746
Epoch 20/20
21/21 [==============================] - 0s 7ms/step - loss: 0.2213 - accuracy: 0.9223 - val_loss: 0.3413 - val_accuracy: 0.8785# loss 값을 plot 해보겠습니다.
y_vloss = history.history['val_loss']
y_loss = history.history['loss']
x_len = np.arange(len(y_loss))
plt.plot(x_len, y_vloss, marker='.', c='red', label="Validation-set Loss")
plt.plot(x_len, y_loss, marker='.', c='blue', label="Train-set Loss")
plt.legend(loc='upper right')
plt.grid()
plt.ylim(0,1)
plt.title('Loss graph with batch normalization')
plt.xlabel('epoch')
plt.ylabel('loss')
plt.show()
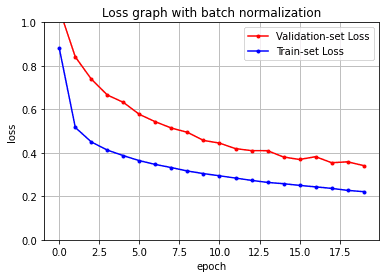
# accuracy 값을 plot 해보겠습니다.
y_vacc = history.history['val_accuracy']
y_acc = history.history['accuracy']
x_len = np.arange(len(y_acc))
plt.plot(x_len, y_vacc, marker='.', c='red', label="Validation-set accuracy")
plt.plot(x_len, y_acc, marker='.', c='blue', label="Train-set accuracy")
plt.legend(loc='lower right')
plt.grid()
plt.ylim(0.5,1)
plt.title('Accurcy graph with batch normalization')
plt.xlabel('epoch')
plt.ylabel('accuracy')
plt.show()