선형대수 기초 및 numpy 적용

행렬의 계산, 종류, numpy 내부 메서드를 다룬다.

1. 행렬의 계산

• 행렬

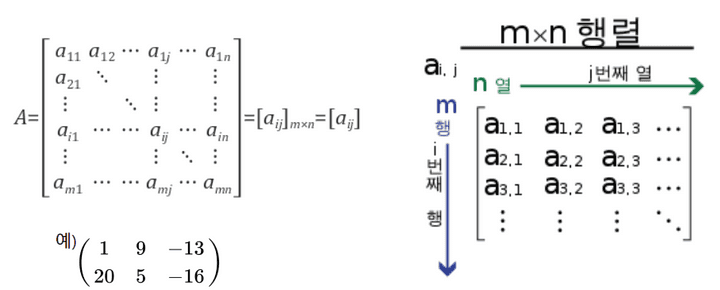
• 행렬 + 행렬

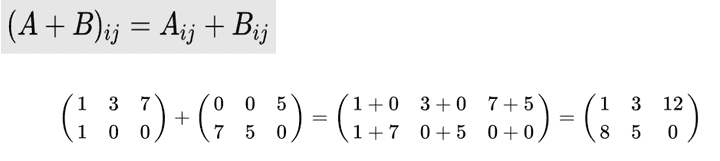
• 스칼라 * 행렬

: 각 자리마다 스칼라를 곱한다

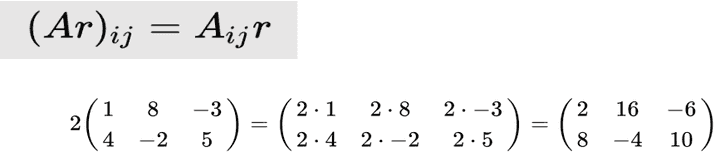
• 행렬 * 행렬

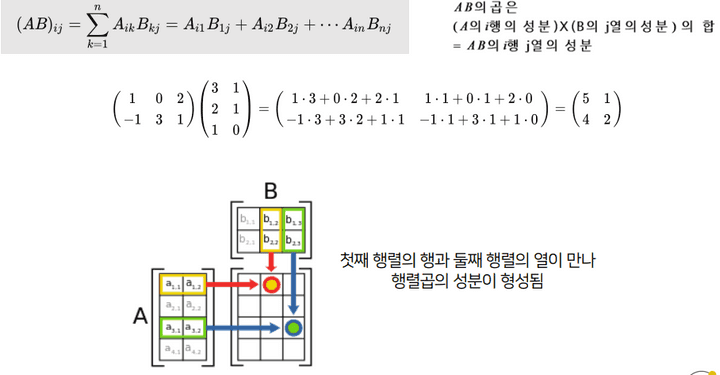
A 의 열 값과 B 의 행 값이 같아야 한다 → A의 행 , B의 열 을 가진 새로운 행렬 탄생

dot product / 내적 이라고도 표현한다.

그림을 보면, A(4,2) 와 B(2,3) 이 만나 (4,3) 이 된다.

곱은 이렇게 이루어진다.

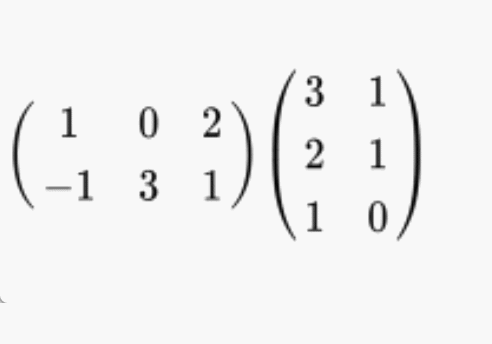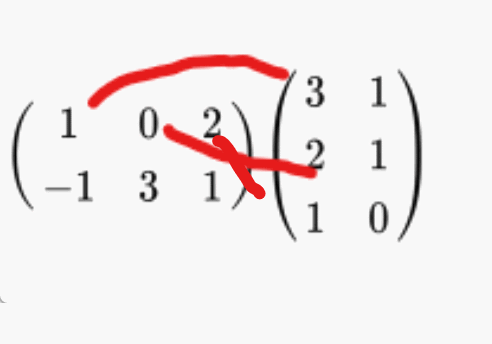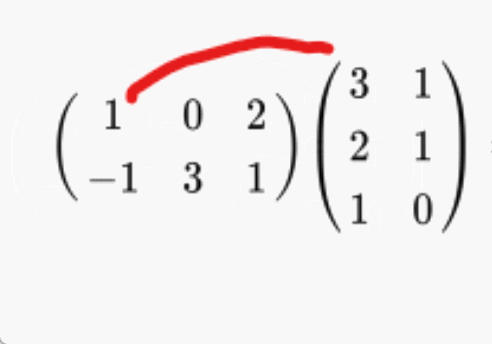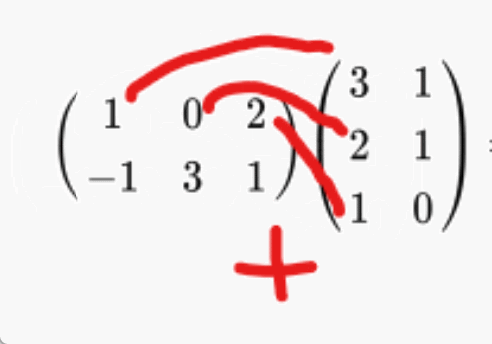
1*3 + 0*2 + 2*1

다음의 계산을 2 x 2 번 반복해서 2열 2행의 값이 나온다,

2. 행렬의 종류

• 전치 행렬

: 행과 열이 바뀐 행렬

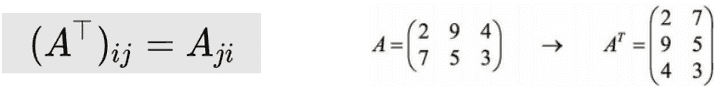
전치행렬의 성질

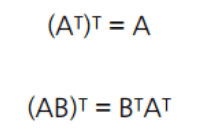
• 영행렬

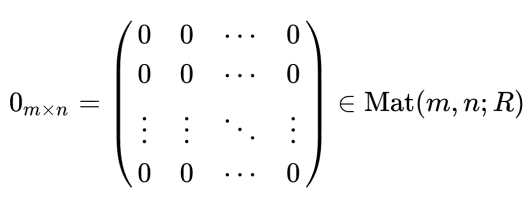
R 은 실수(real)

• 단위 행렬

: 대각선만 1인 행렬

기호는 I, E 둘 다 쓴다.

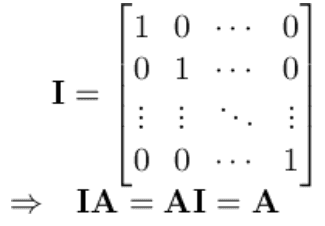
• 대각 행렬

: 대각선만 특정 수로 채워진 행렬 (특정 수는 행마다 다를 수 있음. )

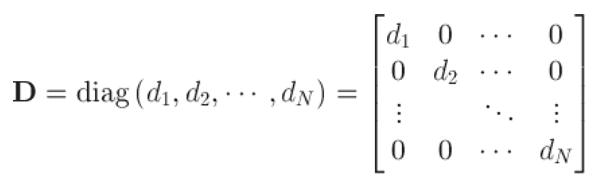
3. matmul 과 dot 의 차이

→ 다시 말해서

matmul() : 맨 마지막 두 행의 l x m , m x k ⇒ l x k 로 만든다 : 차원 수는 동일해진다

dot : A 의 맨 마지막 차원 수 m 과 B 의 마지막에서 두번째 차원 수 m 를 없앤다. 결국 차원이 늘어난다.

4. linspace 와 arrange 의 차이

arange() 함수에서는 간격을 지정

linspace()함수에서는 구간의 개수를 지정

arrange 는 어느 step 만큼 수를 키울 것인지 를 파라미터로 받는다

linspace 는 start - end 사이에 들어갈 숫자의 개수를 파라미터로 받는다